Изначально воспользуемся общей методикой определения АЧХ и ФЧХ функции:
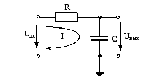
Рис.2.4 Последовательное соединение RC ‑ цепи
Определение комплексной функции цепи (КФЦ):
Так как в лабораторной работе№4 исследуются передаточные характеристики, то будем определять КФЦ коэффициента передачи по напряжению.
Согласно определению (выражение (2.1)) коэффициент передачи – это отношение выходного напряжения ко входному:
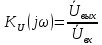 (2.9а)
(2.9а)
По закону Ома входное напряжение 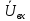 определяется:
определяется:
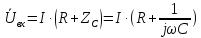
В свою очередь, также по закону Ома, напряжение на выходе определяется напряжением на емкости, которое определяется следующим образом:
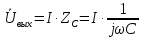
Тогда коэффициент передачи по напряжению будет иметь вид:
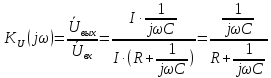
Приведем знаменатель к стандартному виду, т.е. избавимся от «многоэтажного» выражения.
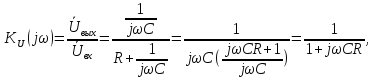
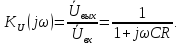 (2.9)
(2.9)
Выражение (2.9) является передаточной комплексной функцией цепи
Определение выражения АЧХ:
Согласно определению и выражению (2.5) АЧХ функции – это модуль функции или отношение модулей числителя и знаменателя для комплексных выражений. Тогда из выражения (2.9) выделим модуль:
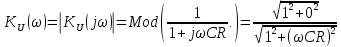 ,
,
Таким образом, АЧХ коэффициента передачи имеет вид (2.10):
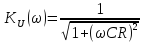 , (2.10)
, (2.10)
где R,C – параметры цепи, ω – круговая частота входного воздействия: 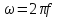 .
.
Определение выражения ФЧХ:
Исходя из общего определения и математической записи (2.7) ФЧХ исследуемой цепи, определим для исследуемой схемы фазо-частотную характеристику (ФЧХ). Для этого необходимо найти главный аргумент КФЦ. В соответствии с теорией комплексных выражений, аргумент выражения равен разности аргументов числителя и знаменателя. Запишем сказанное математически:
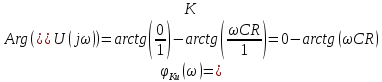 ,
,
Таким образом, ФЧХ коэффициента передачи имеет вид (2.11):
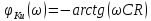 . (2.11)
. (2.11)
Для того, чтобы графически изобразить АЧХ и ФЧХ передаточной функции (или по-другому, коэффициента передачи), необходимо вместо параметров цепи подставить номиналы элементов, а вместо круговой частоты 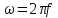 подставить соответствующие значения, при разных значениях циклической частоты, например, 0, 200Гц, 1кГц, 1.25кГц, 2,5кГц, 5кГц, 10кГц, 20 кГц.
подставить соответствующие значения, при разных значениях циклической частоты, например, 0, 200Гц, 1кГц, 1.25кГц, 2,5кГц, 5кГц, 10кГц, 20 кГц.
2.4 Определение характера частотных характеристик цепи (ачх и фчх) на основе схемы без вывода выражений ачх и фчх
Следует отметить, что целью лабораторной работы является исследование частотных характеристик в цепях первого порядка (в составе схемы не более одной реактивности). В таких цепях невозможны экстремумы функций частотных характеристик, т.е. характер функции монотонный, а, значит, предполагаемый характер частотных характеристик может быть изображен на основе анализа схемы на крайних частотах диапазона и .
Исследуем схему на рис.2.4 на крайних частотах:
1) Построение АЧХ по схеме [3]:
Так как в схеме один реактивный элемент, ЧХ цепи будут монотонными функциями частоты и для их изображения достаточно знать значения ЧХ на крайних частотах диапазона и
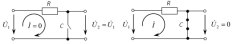
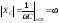
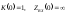
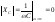
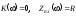
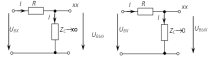
Рис.2.5 — Схемы замещения исследуемой цепи
на крайних частотах диапазона
По полученным результатам построим АЧХ исследуемой цепи (рис.2.6):

Рис. 2.6- АЧХ передаточной функции исследуемой цепи
2) Построение ФЧХ коэффициента передачи:
Для построения ФЧХ непосредственно на основе схемы необходимо сохранить характер реактивного сопротивления. Поэтому эквивалентные схемы изобразим не для = 0, а для 0, не для a для
 0
0
Рис. 2.7 Схема замещения участка цепи для определения ФЧХ
В соответствии с определением коэффициента передачи по напряжению 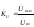 .
.
Следовательно, 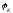 =
= 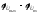 .
.
Для удобства положим 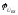 = 0, тогда
= 0, тогда 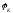 =
= 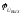
Построим векторные диаграммы для схемы рисунка 2.7а и б, соответственно:
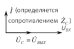

Рис. 2.8 Векторные диаграммы напряжений на граничных частотах
Исходя из рис.2.8а, разность фаз между входным и выходным напряжениями составило 0 0 , т.е.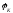 (0) = 0 o . Согласно рис.2.8 вектор. напряжения выхода отстает от вектора входного напряжения на 90 0 , а значит,
(0) = 0 o . Согласно рис.2.8 вектор. напряжения выхода отстает от вектора входного напряжения на 90 0 , а значит,  ( = -90 0 . По полученным данным построим ФЧХ коэффициента передачи:
( = -90 0 . По полученным данным построим ФЧХ коэффициента передачи:
Пример 1.1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис.1.4) рассчитать ее частотные характеристики.
1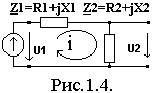 . Zвх(j), Zвх(), z(). 2. K(j), K(), k().
. Zвх(j), Zвх(), z(). 2. K(j), K(), k().
Решение. 1) По определению Zвх(j)=Ů1m/ .Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:
.Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:
Z вх()=[(R1+R2)²+(X1+X2)²] 1/2 ; z()=arctg[(X1+X2)/(R1+R2)].
вх()=[(R1+R2)²+(X1+X2)²] 1/2 ; z()=arctg[(X1+X2)/(R1+R2)].
2) Используя определение К(j) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:
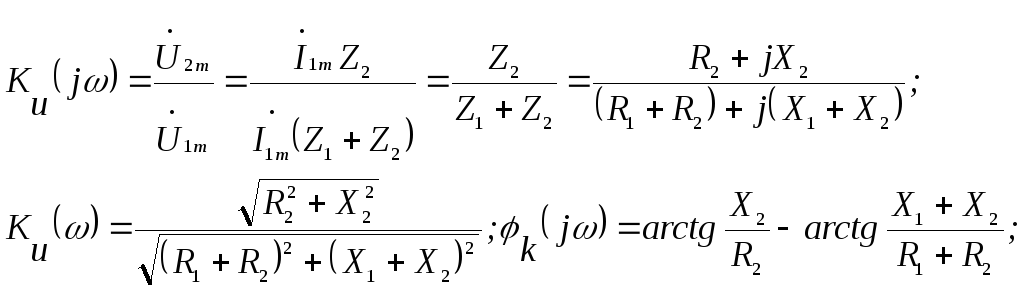
Пример 1.2. Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис.1.5), рассчитать ее частотные характеристики:
1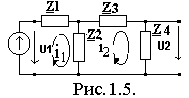 . Zвх(j), Zвх(), z(). 2.K(j), K(), k().
. Zвх(j), Zвх(), z(). 2.K(j), K(), k().
Решение. 1) Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.
П о определению Zвх(j)=Ů1m/
о определению Zвх(j)=Ů1m/ .Входное сопротивление находимметодом последовательных эквивалентных преобразований. Этот метод состоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.1.6.
.Входное сопротивление находимметодом последовательных эквивалентных преобразований. Этот метод состоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.1.6.
2. найдем КЧХ коэффициента передачи по напряжению. По определения Ku(j)=Ů2m/Ů1m, а Ů2m=Z4Ĭ2– находим по закону Ома.
Отсюда видно, что для расчета КЧХ необходимо найти Ĭ2. Находим Ĭ2 методом контурных токов. Для этого: определим число независимых контуров: Nk=в-у+1=3-2+1=2, каждому из них присвоим свой контурный ток I1, I2 и составим уравнения по методу контурных токов.
Z 11Ĭ1+Z12Ĭ2=E11
11Ĭ1+Z12Ĭ2=E11
где: Z11 – собственное сопротивление первого контура, Z11=Z1+Z2;
E22— алгебраическая сумма источников ЭДС II-ого контура, во II контуре источников ЭДС нет, E22=0. Найдем I2— ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:
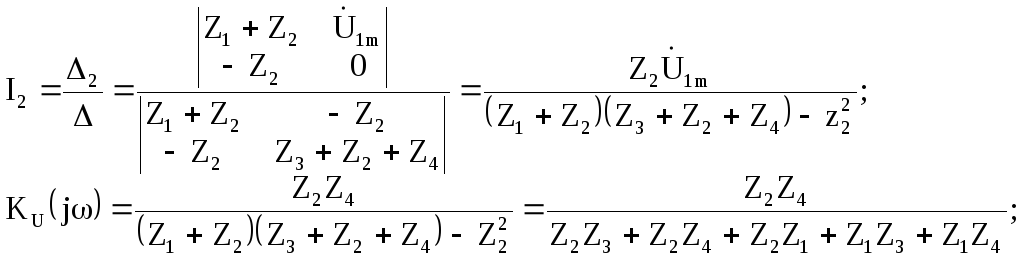
Покажем другой способ нахождения КЧХ коэффициента передачи по напряжению. Найдем КЧХ, используя для расчета U2m метод узловых потенциалов. Для этого:
преобразуем исходную схему к виду показанному на рис.1.7, заменив источник эдс на источник тока;
потенциал узла 0 примем равным нулю, =0;
т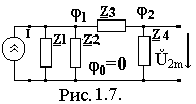 огда Ů2m=2 — = 2.
огда Ů2m=2 — = 2.
Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее, относительно 2, по методу Крамера:
Y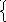 111+ Y122=I11
111+ Y122=I11
1, 2 – потенциалы первого и второго узлов;
I 11, I11 – токи источников токов сходящихся в первом и втором узлах.
11, I11 – токи источников токов сходящихся в первом и втором узлах.
Отсюда следует, что
П ример 1.3. Для цепи изображенной на рис.1.8 рассчитать:
ример 1.3. Для цепи изображенной на рис.1.8 рассчитать:
О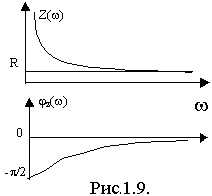 т исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.1.4.
т исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.1.4.
Используя, определение zвх(j) и законы Ома и Кирхгофа получим его выражение 
О пределим АЧХ и ФЧХ дляzвх(j) и построим ихграфики (рис.9), подсчитав значения при =0, =.
пределим АЧХ и ФЧХ дляzвх(j) и построим ихграфики (рис.9), подсчитав значения при =0, =.
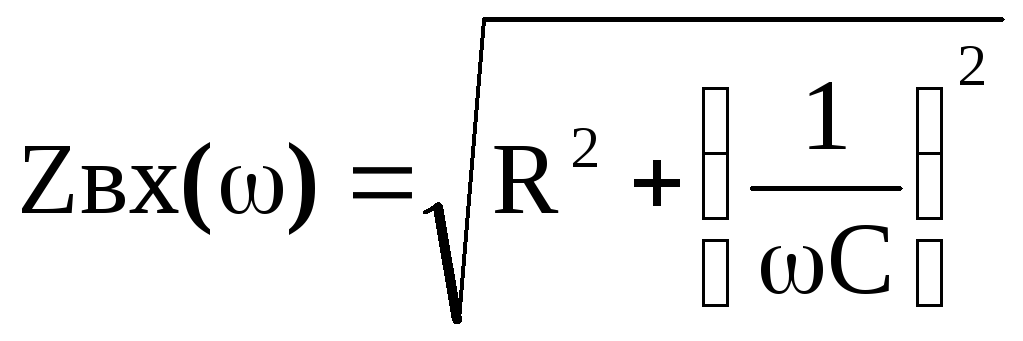 ; Zвх(0) = . Zвх() = R.
; Zвх(0) = . Zвх() = R.
z()= -arctg  , z(0)=-/2, z()=0.
, z(0)=-/2, z()=0.
Используя, определение KU(j) получим его выражение Ku(j)=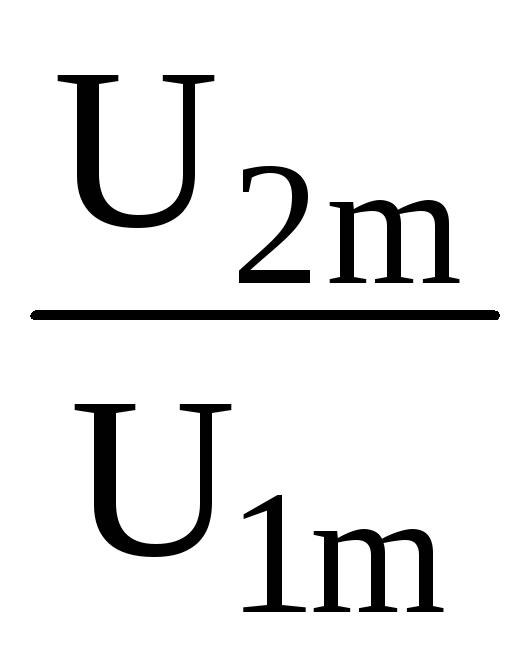 =
=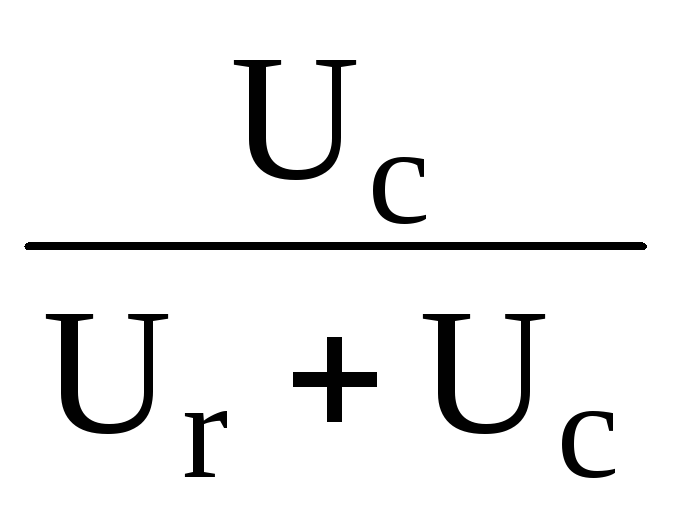 =
=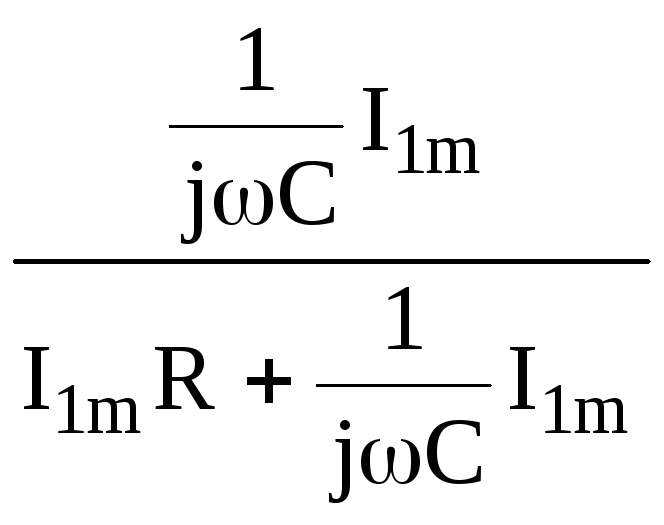 =
=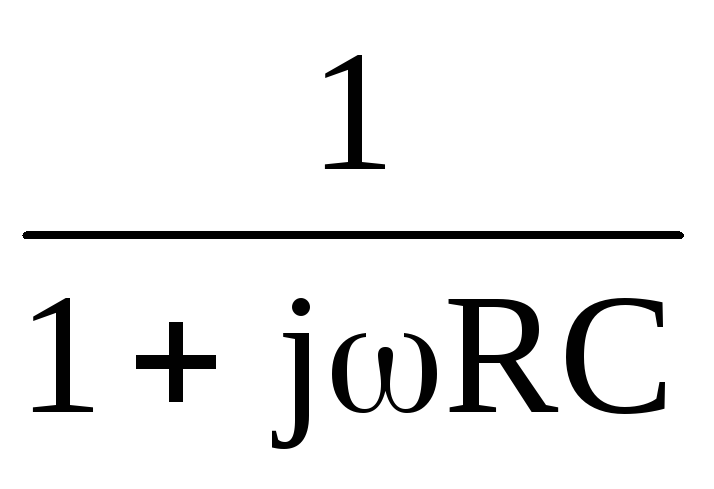 .
.
Определим АЧХ и ФЧХ для Ku (j) и построим их графики (рис.1.10), подсчитав значения при =0, =.
Вспомним, что z=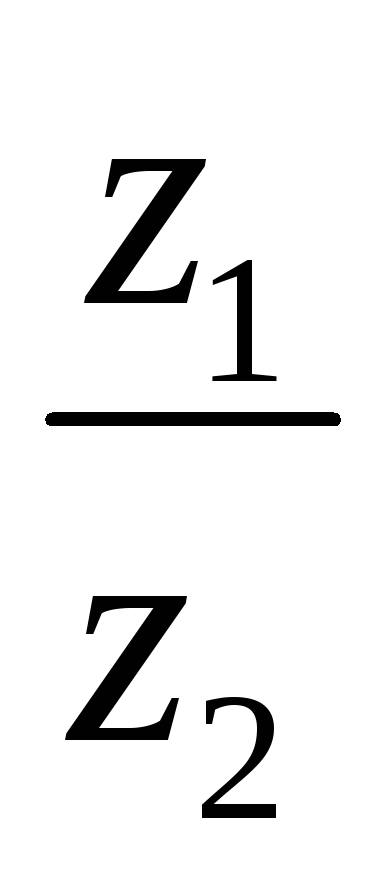 =
=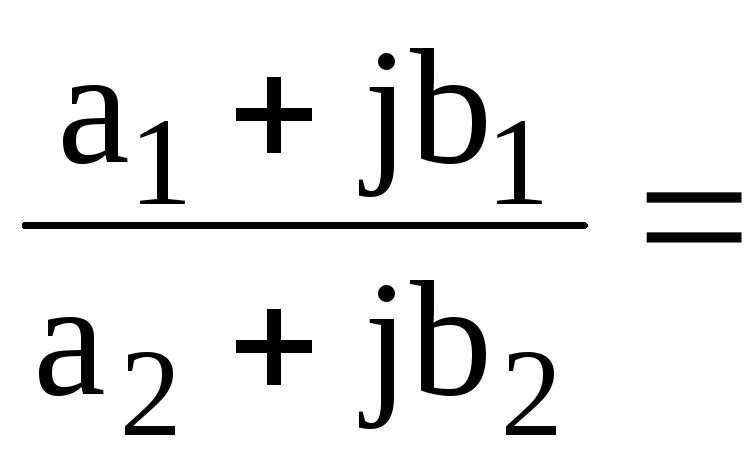
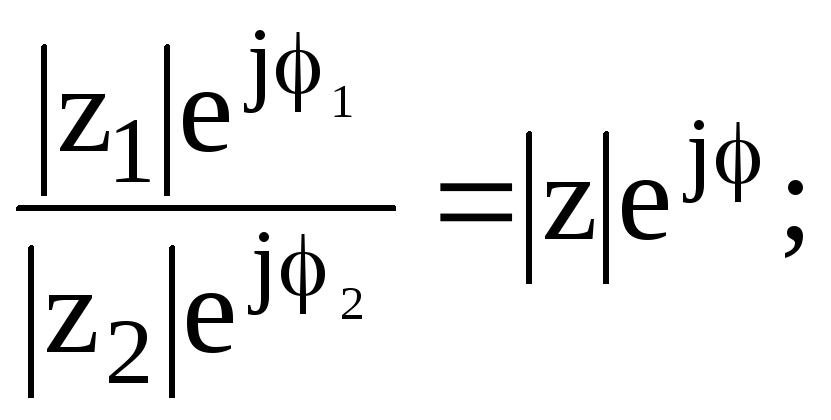 где:
где: 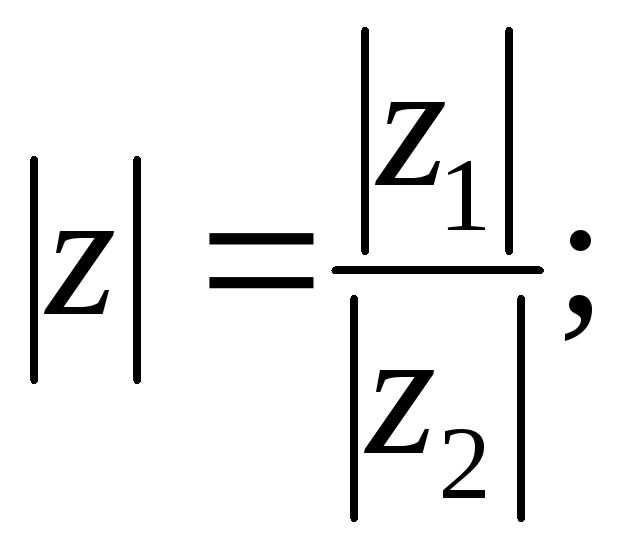
 тогда,
тогда,
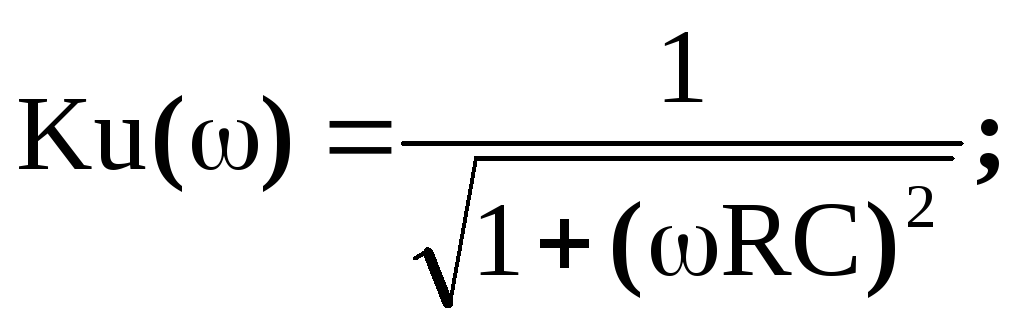 Ku(0)=1; Ku()=0.
Ku(0)=1; Ku()=0.
О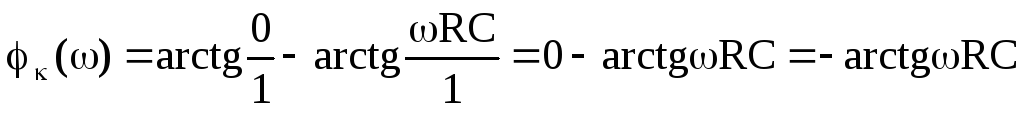 тсюда следует: φк()= π/2, φк(0)= 0.
тсюда следует: φк()= π/2, φк(0)= 0.
Такая цепь пропускает сигналы низких частот (Ku(0)=1) и подавляет сигналы высоких частот (Ku()=0) и называется фильтром низких частот (ФНЧ).
Г раничная частота определяется из выражения
раничная частота определяется из выражения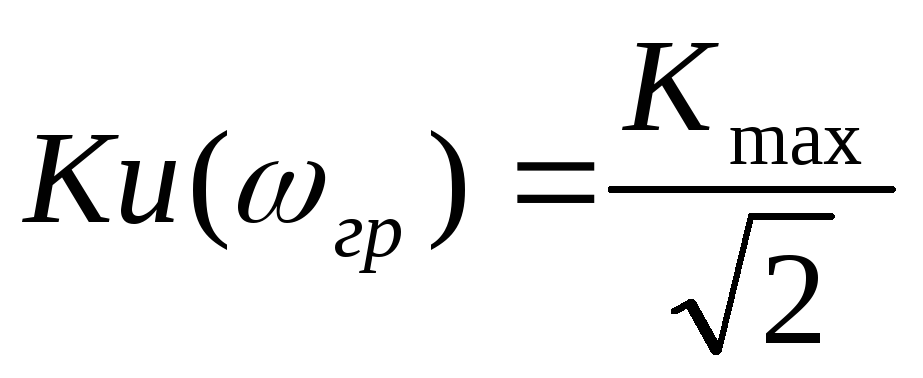 . Рассчитаем ее для нашего примера:
. Рассчитаем ее для нашего примера:
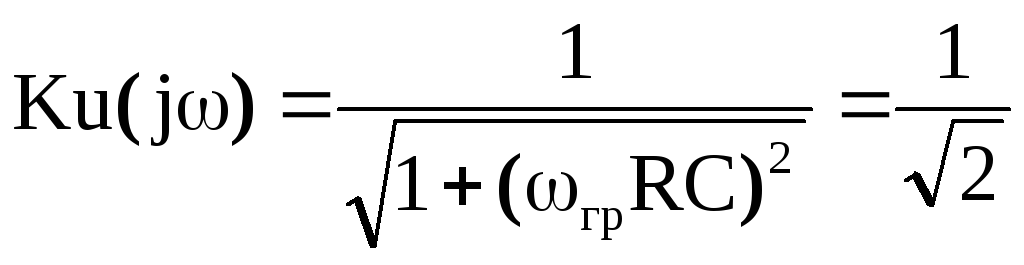 , грRC=1
, грRC=1 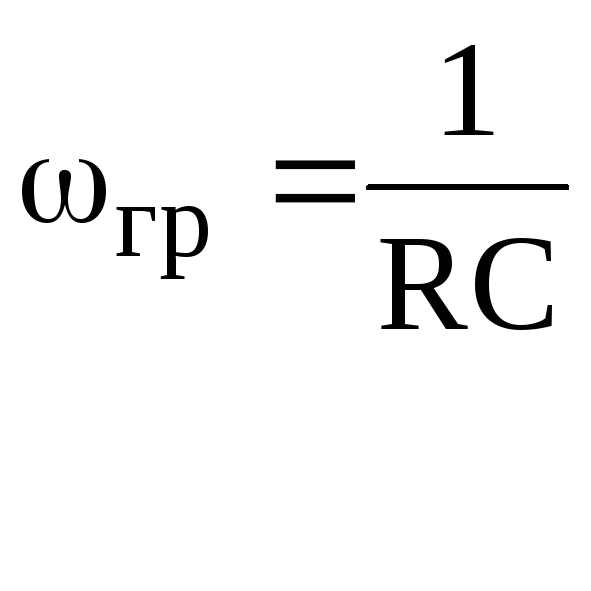 .
.
Пример 1.4. Условия прежние. Схема приведена на рис. 1.11.
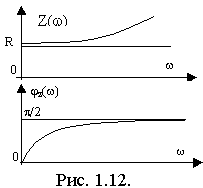
Найдем комплексную функцию входного сопротивления, а также ее АЧХ и ФЧХ и построим графики (рис.1.12).
 От исходной цепи переходим к ее комплексной схеме замещения (рис.1.4). Далее, по аналогии с предыдущем, найдем интересующие нас частотные зависимости:
От исходной цепи переходим к ее комплексной схеме замещения (рис.1.4). Далее, по аналогии с предыдущем, найдем интересующие нас частотные зависимости:
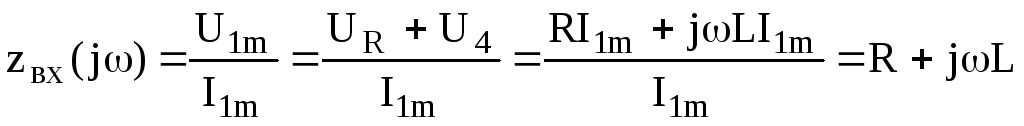 ;
; 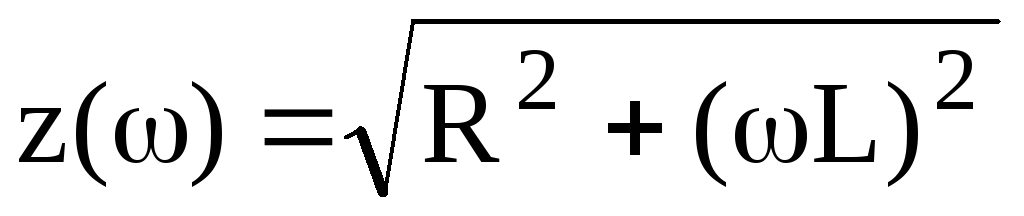 , z(0)=R; z()=.
, z(0)=R; z()=.
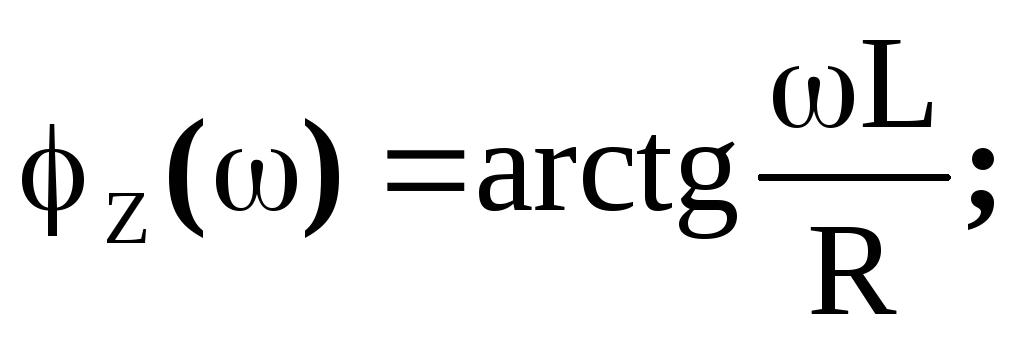 ,,z(0)=0 ,z()=.
,,z(0)=0 ,z()=.
П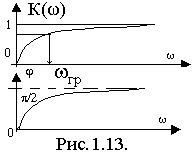 олучим выражения для KU(j), KU(), k(ω).
олучим выражения для KU(j), KU(), k(ω). 
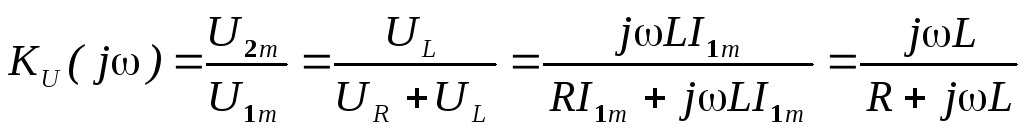
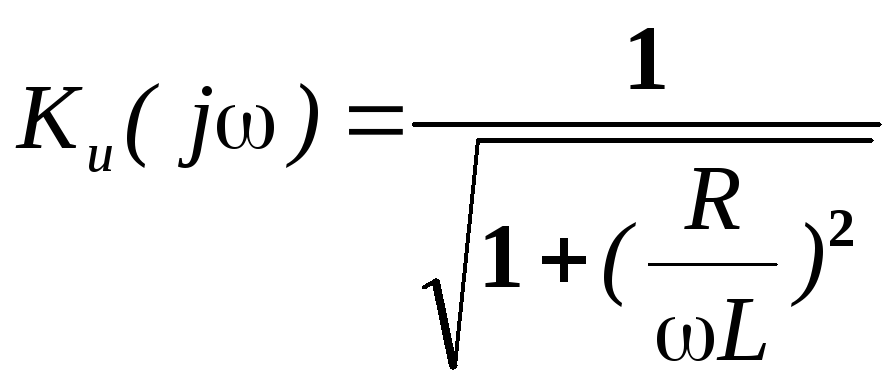 , Ku(0)=0, Ku()=1.
, Ku(0)=0, Ku()=1.
Графики зависимостей KU(), k(ω) приведены на рис.1.13.


Эта цепь, пропускающая сигналы высоких частот и подавляющая сигналы низких частот называется фильтром высоких частот (ФВЧ).
Определим граничную частоту. По определению 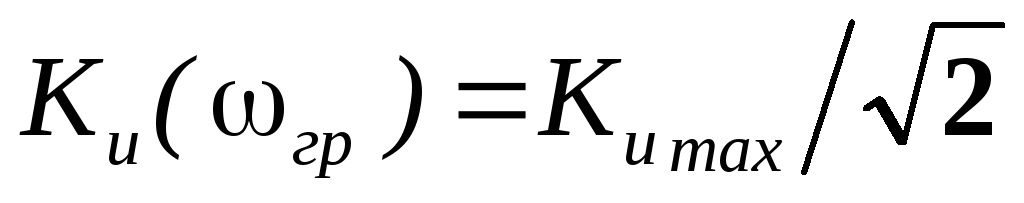 . Отсюда:
. Отсюда:
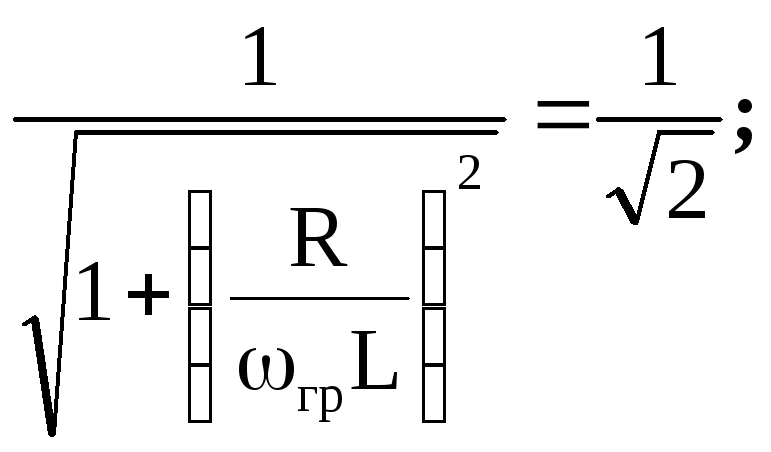
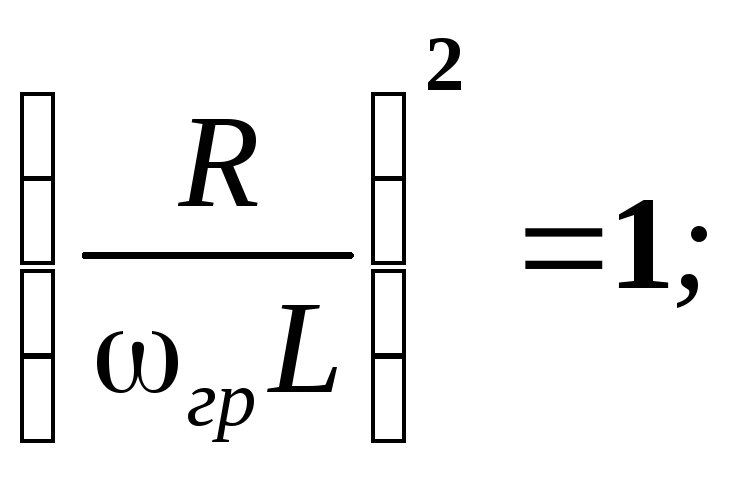
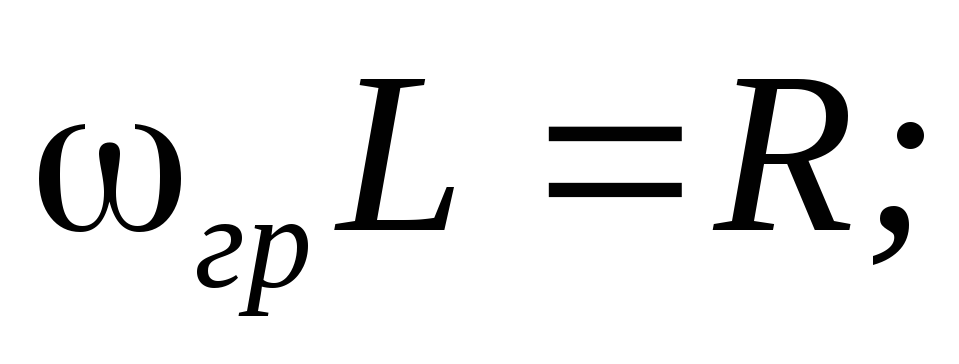
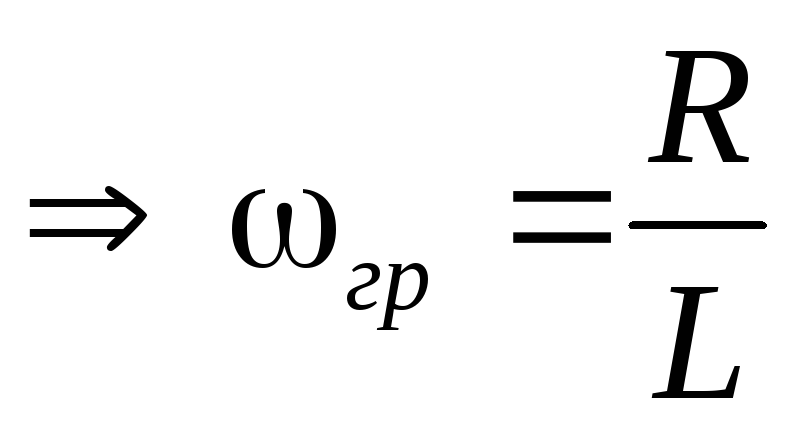 .
.
Пример 1.5. Для цепи (рис.1.14) определить комплексную функцию входного сопротивления Zвх(j), ее АЧХ — Zвх() и ФЧХ — 2().
Д ано: R1=1кОм R2=2кОм; R3=2кОм; C=1мкФ; L=10 -2 Гн.
ано: R1=1кОм R2=2кОм; R3=2кОм; C=1мкФ; L=10 -2 Гн.
Решение. Комплексную функцию входного сопротивления находим методом эквивалентных преобразований, перейдя к комплексной схеме замещения (рис.1.5).
На первом этапе преобразуем участок цепи, содержащий последовательное соединение элементов L и R3. Получим выражение для их комплексного сопротивления Z34=jL+R3.
На втором этапе преобразуем участок цепи, состоящий из параллельно соединенных элементов R2 и Z34. Получим 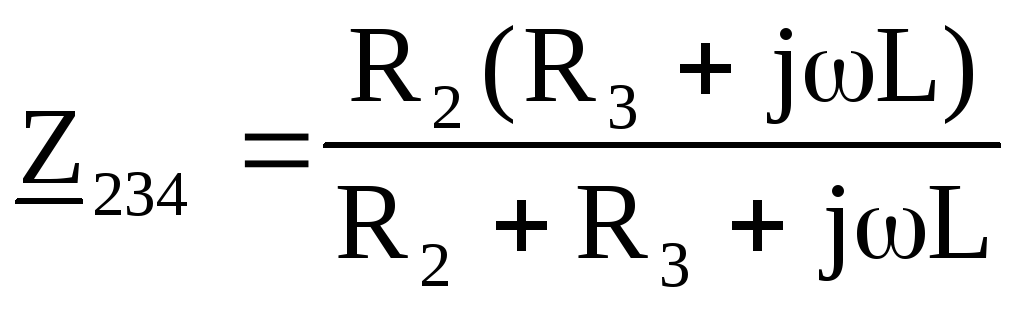 .
.
На третьем, заключительном, этапе преобразуем участок цепи, содержащий последовательное соединение ветви Z1, состоящей из последовательного соединения R1 и C и участка цепи с сопротивлением Z234. Получим
 .
.
Запишем полученное выражение в алгебраической форме:
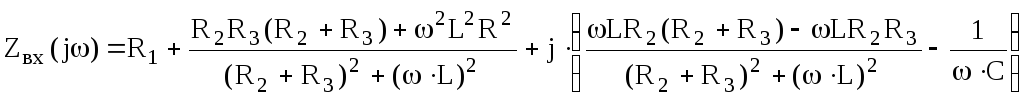 .
.
Отсюда выражения для АЧХ и ФЧХ имеют вид:
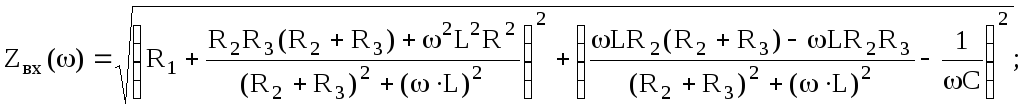
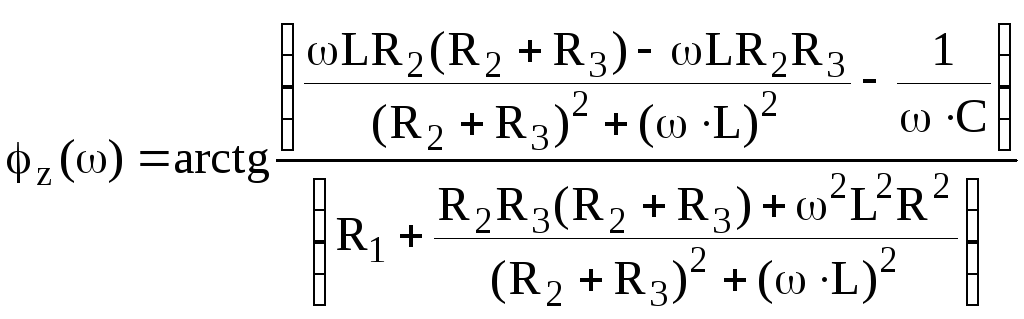 .
.
К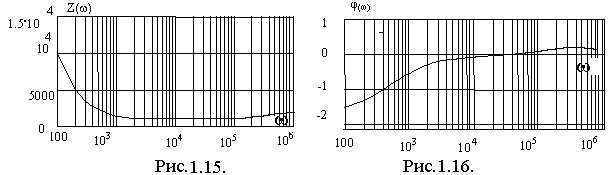 ачественный анализ схемы показывает, что при=0, т.к. Xс= — входное сопротивление — равно бесконечности, а при , т.к. XC=0, XL=, входное сопротивление равно R1+R2. Это совпадает с расчетом по полученным выражениям, что подтверждает их правильность.
ачественный анализ схемы показывает, что при=0, т.к. Xс= — входное сопротивление — равно бесконечности, а при , т.к. XC=0, XL=, входное сопротивление равно R1+R2. Это совпадает с расчетом по полученным выражениям, что подтверждает их правильность.
Результаты расчета АЧХ и ФЧХ представлены на графиках (рис.1.15 и 1.16). При этом значение частоты взято в логарифмическом масштабе т.е. lg .
Пример 1.6. Для цепи (рис.1.14), используя метод контурных токов, вывести выражения для комплексной функции коэффициента передачи напряжений Ku(j) (его АЧХ — Ku() и ФЧХ — k()) и построить графики АЧХ и ФЧХ.
Решение. Топологический анализ показывает: число узлов nу=2, число ветвей nв=3. Отсюда число независимых контуров Nв=nу-nв+1=3-2+1=2. Выбираем направление обхода контуров, как правило, по часовой стрелке. Вводим обозначения и направления контурных токов 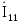 и
и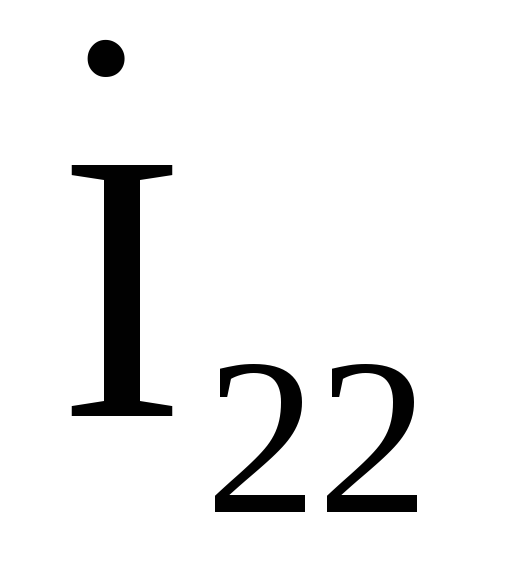 , как показано на рис. 1.14.
, как показано на рис. 1.14.
Для нахождения 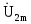 используя МКА необходимо найти ток
используя МКА необходимо найти ток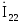 (
(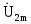 =R3
=R3 ). Система уравнений, составленная по методу контурных токов, имеет вид:
). Система уравнений, составленная по методу контурных токов, имеет вид:
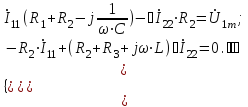
Решая систему по методу Крамера относительно тока 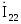 , получаем:
, получаем:
 .
.
Отсюда выражение для комплексного коэффициента передачи напряжения имеет вид:
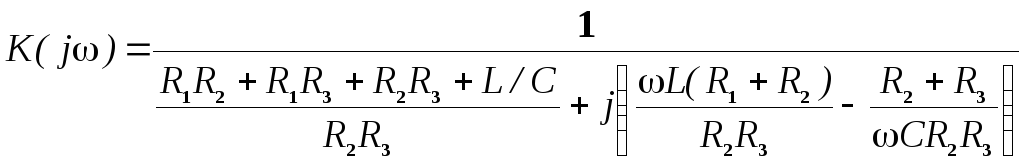 .
.
АЧХ и ФЧХ соответственно равны:
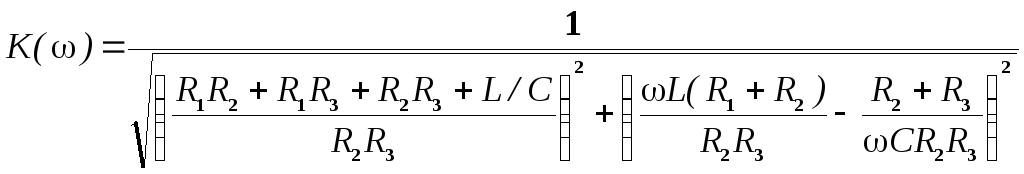 ;
;
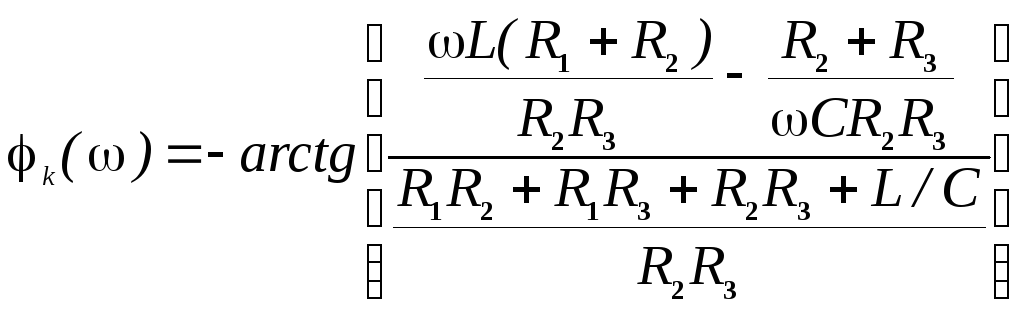 .
.
К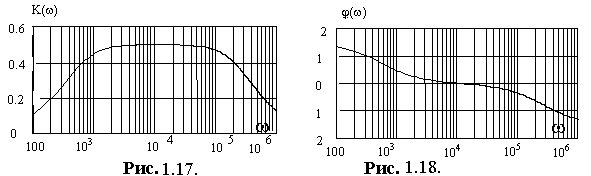 ачественный анализ схемы показывает, что при=0, т. к. XC(), то U2m=0, т.е. Ku(0)=0. При =, XL(), а потому U2m=0, т.е. Ku()=0. Это ты совпадает с расчетом по полученным выражениям для АЧХ, что подтверждает правильность проведенных расчетов.
ачественный анализ схемы показывает, что при=0, т. к. XC(), то U2m=0, т.е. Ku(0)=0. При =, XL(), а потому U2m=0, т.е. Ku()=0. Это ты совпадает с расчетом по полученным выражениям для АЧХ, что подтверждает правильность проведенных расчетов.
Результаты расчета АЧХ и ФЧХ представлены на графиках (рис.1.17 и 1.18). При этом значения частоты взяты в логарифмическом масштабе, т.е. lg.
Пример 1.7. Решить пример 1.6 методом узловых потенциалов.
Решение. Схема содержит три узла (nу=3). Пронумеруем узлы и введем их обозначения (рис.1.14). Для нахождения U2m необходимо определить 2=U2m. Система уравнений, для нахождения 2, составленная по методу узловых потенциалов, имеет вид:
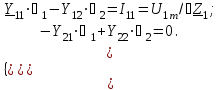
где 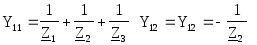 ,
,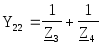 .
.
Решая эту систему относительно 2 по методу Крамера, получим:
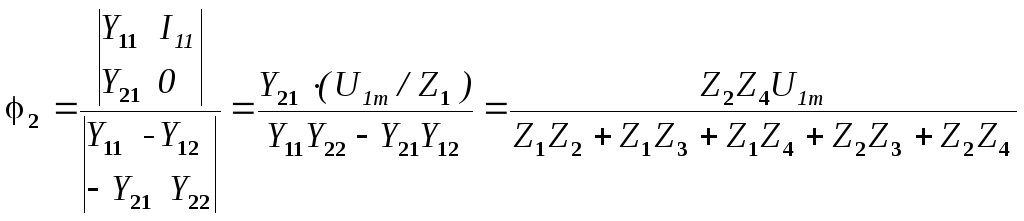 .
.
Отсюда, после подстановок, получим выражение для комплексного коэффициента передачи напряжения:
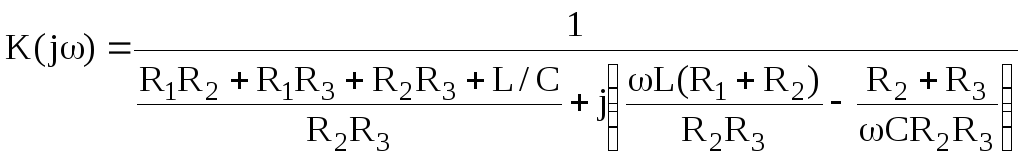 .
.
АЧХ и ФЧХ соответственно равны:
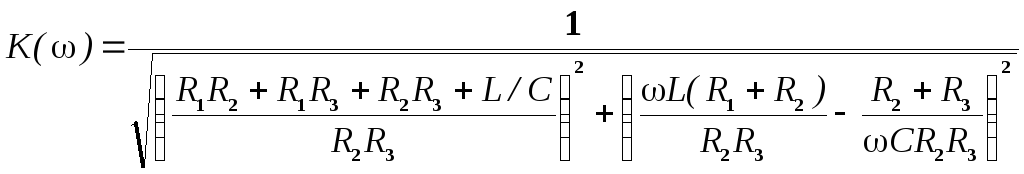 ,
,
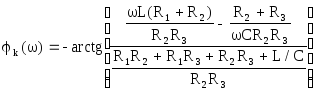 .
.
Сопоставляя результаты расчета в данном примере с результатами предыдущего примера, видим их полное совпадение. Это подтверждает правильность наших расчетов.
Пример 1.1. Для обобщенной одноконтурной цепи, представленной комплексной схемой замещения (рис.1.4) рассчитать ее частотные характеристики.
1 . Zвх(j), Zвх(), z(). 2. K(j), K(), k().
. Zвх(j), Zвх(), z(). 2. K(j), K(), k().
Решение. 1) По определению Zвх(j)=Ů1m/ .Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:
.Используя законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления:
Z вх()=[(R1+R2)²+(X1+X2)²] 1/2 ; z()=arctg[(X1+X2)/(R1+R2)].
вх()=[(R1+R2)²+(X1+X2)²] 1/2 ; z()=arctg[(X1+X2)/(R1+R2)].
2) Используя определение К(j) и законы Ома и Кирхгофа, найдем КЧХ, а также АЧХ и ФЧХ коэффициента передачи по напряжению:
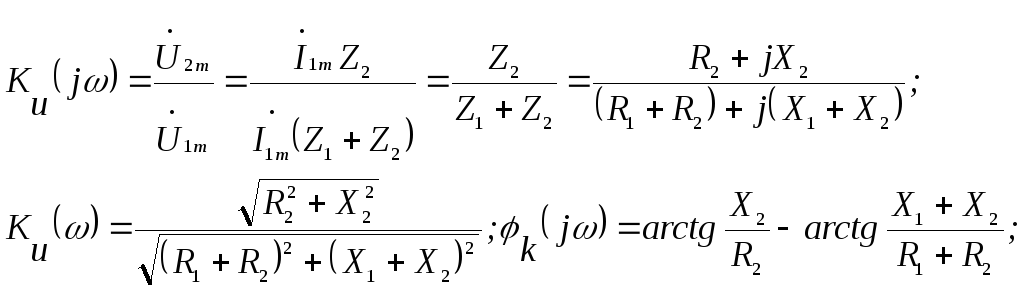
Пример 1.2. Для обобщенной двухконтурной цепи, представленной комплексной схемой замещения (рис.1.5), рассчитать ее частотные характеристики:
1 . Zвх(j), Zвх(), z(). 2.K(j), K(), k().
. Zвх(j), Zвх(), z(). 2.K(j), K(), k().
Решение. 1) Найдем КЧХ, а также АЧХ и ФЧХ входного сопротивления.
П о определению Zвх(j)=Ů1m/
о определению Zвх(j)=Ů1m/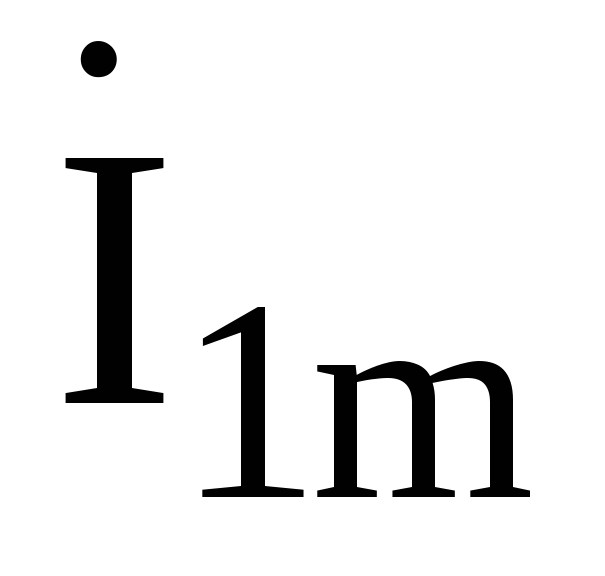 .Входное сопротивление находимметодом последовательных эквивалентных преобразований. Этот метод состоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.1.6.
.Входное сопротивление находимметодом последовательных эквивалентных преобразований. Этот метод состоит в поэтапном преобразовании простых участков цепи. Они показаны на рис.1.6.
2. найдем КЧХ коэффициента передачи по напряжению. По определения Ku(j)=Ů2m/Ů1m, а Ů2m=Z4Ĭ2– находим по закону Ома.
Отсюда видно, что для расчета КЧХ необходимо найти Ĭ2. Находим Ĭ2 методом контурных токов. Для этого: определим число независимых контуров: Nk=в-у+1=3-2+1=2, каждому из них присвоим свой контурный ток I1, I2 и составим уравнения по методу контурных токов.
Z 11Ĭ1+Z12Ĭ2=E11
11Ĭ1+Z12Ĭ2=E11
где: Z11 – собственное сопротивление первого контура, Z11=Z1+Z2;
E22— алгебраическая сумма источников ЭДС II-ого контура, во II контуре источников ЭДС нет, E22=0. Найдем I2— ток второго контура (по методу Крамера), а затем и КЧХ коэффициента передачи по напряжению:
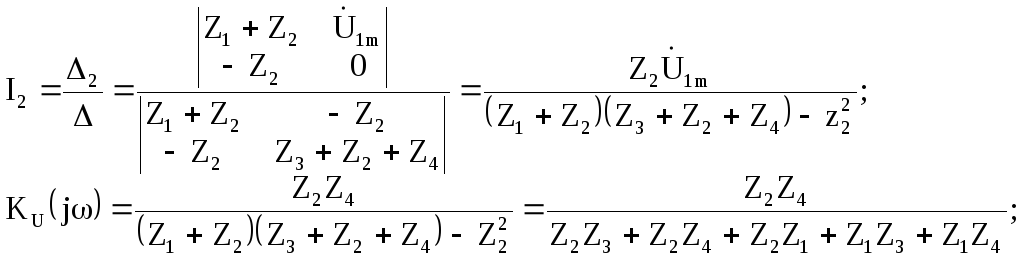
Покажем другой способ нахождения КЧХ коэффициента передачи по напряжению. Найдем КЧХ, используя для расчета U2m метод узловых потенциалов. Для этого:
преобразуем исходную схему к виду показанному на рис.1.7, заменив источник эдс на источник тока;
потенциал узла 0 примем равным нулю, =0;
т огда Ů2m=2 — = 2.
огда Ů2m=2 — = 2.
Составив уравнения по методу узловых потенциалов, получим систему второго порядка и решим ее, относительно 2, по методу Крамера:
Y 111+ Y122=I11
111+ Y122=I11
1, 2 – потенциалы первого и второго узлов;
I 11, I11 – токи источников токов сходящихся в первом и втором узлах.
11, I11 – токи источников токов сходящихся в первом и втором узлах.
Отсюда следует, что
П ример 1.3. Для цепи изображенной на рис.1.8 рассчитать:
ример 1.3. Для цепи изображенной на рис.1.8 рассчитать:
О т исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.1.4.
т исходной цепи переходим к ее комплексной схеме замещения. Она соответствует схеме на рис.1.4.
Используя, определение zвх(j) и законы Ома и Кирхгофа получим его выражение 
О пределим АЧХ и ФЧХ дляzвх(j) и построим ихграфики (рис.9), подсчитав значения при =0, =.
пределим АЧХ и ФЧХ дляzвх(j) и построим ихграфики (рис.9), подсчитав значения при =0, =.
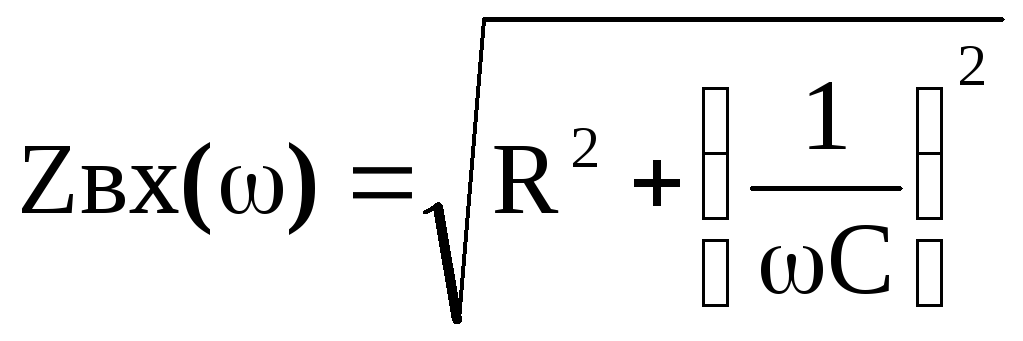 ; Zвх(0) = . Zвх() = R.
; Zвх(0) = . Zвх() = R.
z()= -arctg  , z(0)=-/2, z()=0.
, z(0)=-/2, z()=0.
Используя, определение KU(j) получим его выражение Ku(j)=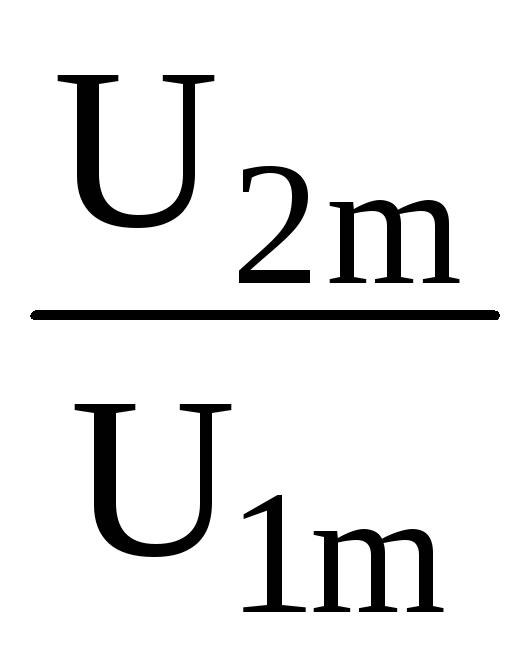 =
=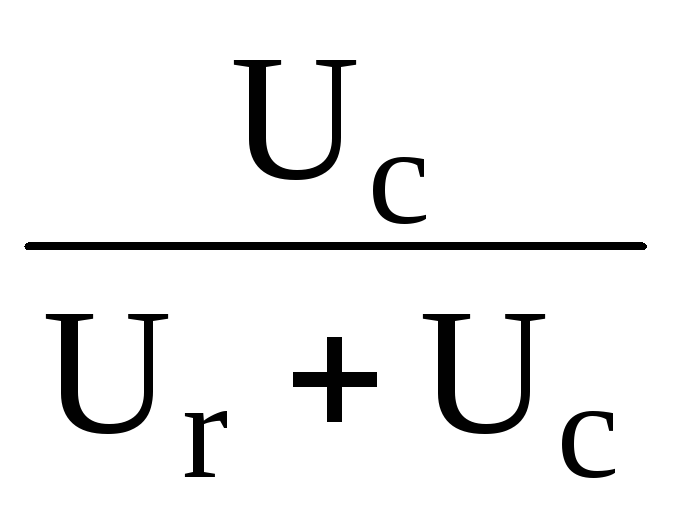 =
=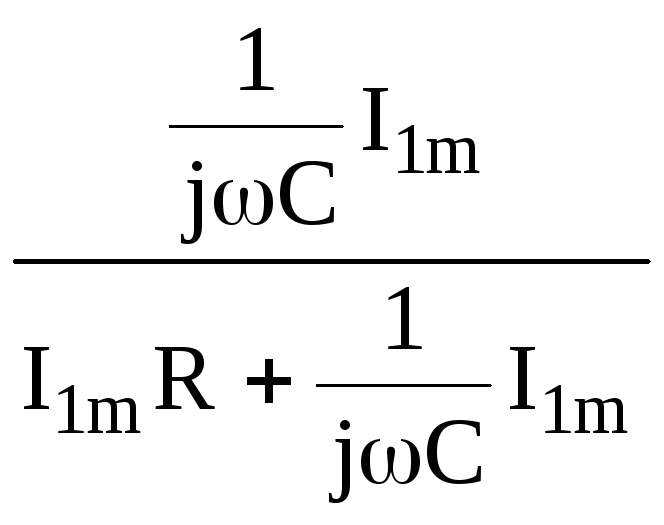 =
=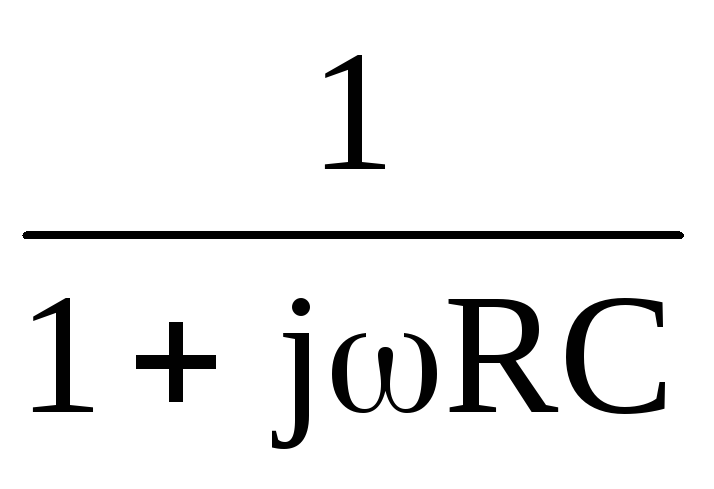 .
.
Определим АЧХ и ФЧХ для Ku (j) и построим их графики (рис.1.10), подсчитав значения при =0, =.
Вспомним, что z=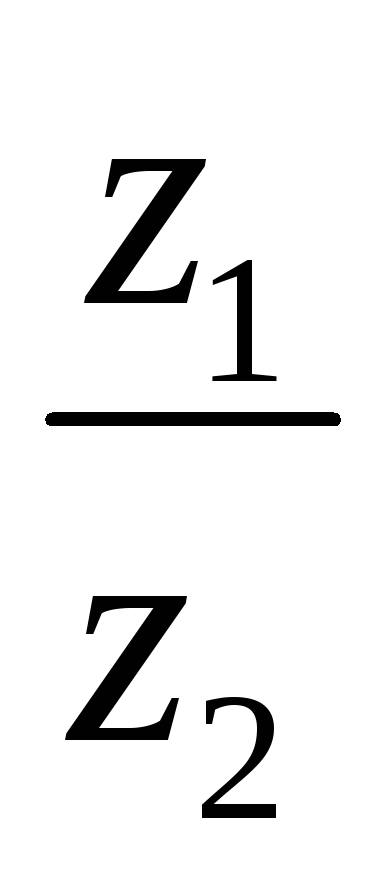 =
=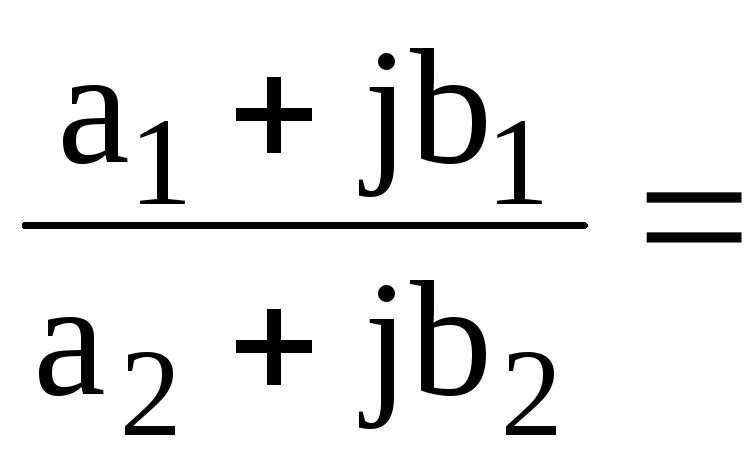
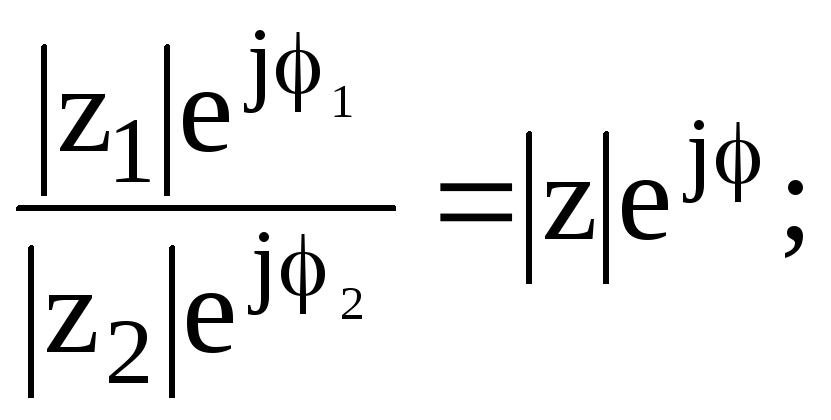 где:
где: 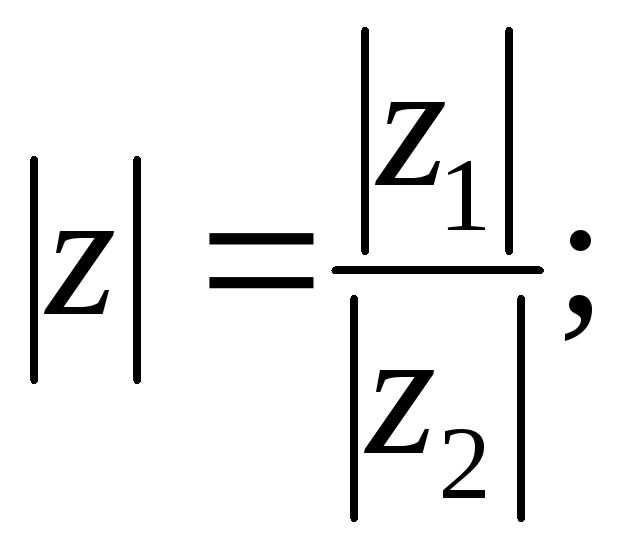
 тогда,
тогда,
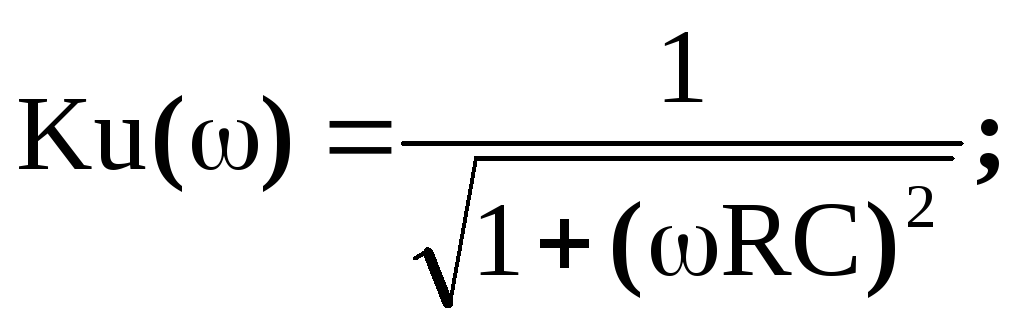 Ku(0)=1; Ku()=0.
Ku(0)=1; Ku()=0.
О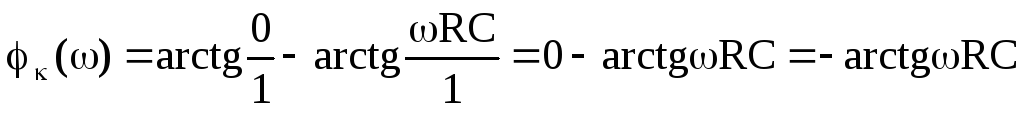 тсюда следует: φк()= π/2, φк(0)= 0.
тсюда следует: φк()= π/2, φк(0)= 0.
Такая цепь пропускает сигналы низких частот (Ku(0)=1) и подавляет сигналы высоких частот (Ku()=0) и называется фильтром низких частот (ФНЧ).
Г раничная частота определяется из выражения
раничная частота определяется из выражения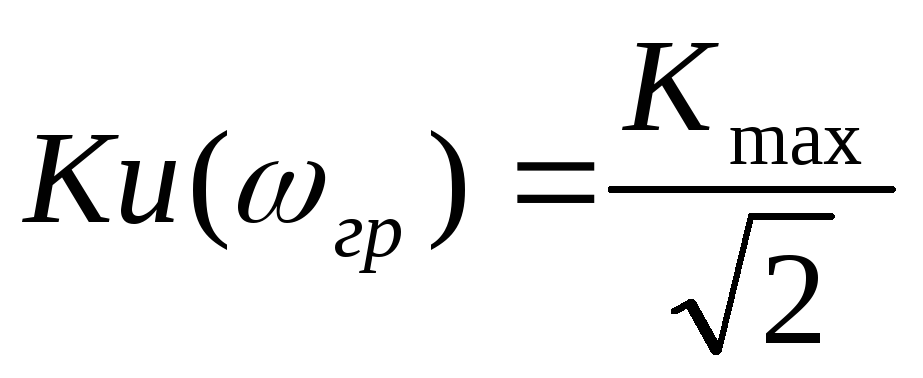 . Рассчитаем ее для нашего примера:
. Рассчитаем ее для нашего примера:
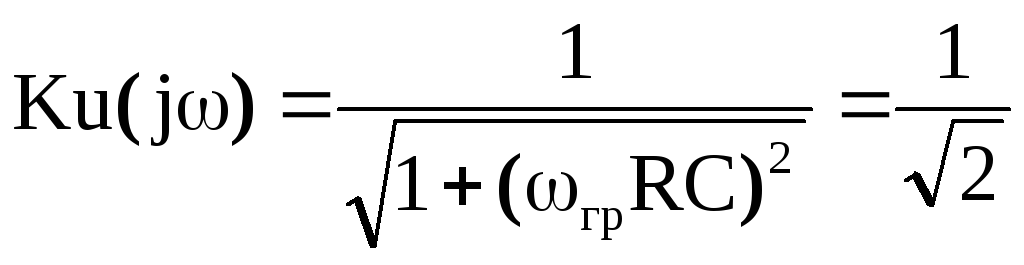 , грRC=1
, грRC=1 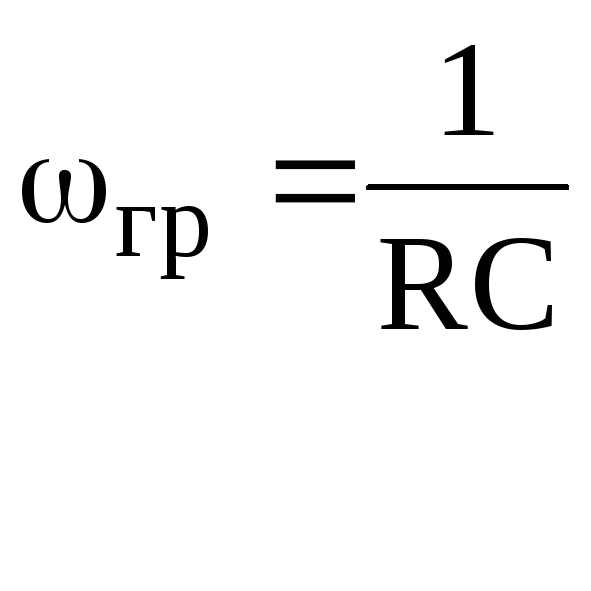 .
.
Пример 1.4. Условия прежние. Схема приведена на рис. 1.11.
Найдем комплексную функцию входного сопротивления, а также ее АЧХ и ФЧХ и построим графики (рис.1.12).
 От исходной цепи переходим к ее комплексной схеме замещения (рис.1.4). Далее, по аналогии с предыдущем, найдем интересующие нас частотные зависимости:
От исходной цепи переходим к ее комплексной схеме замещения (рис.1.4). Далее, по аналогии с предыдущем, найдем интересующие нас частотные зависимости:
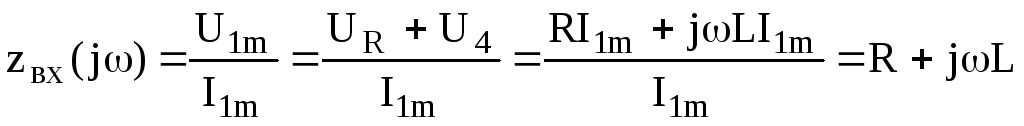 ;
; 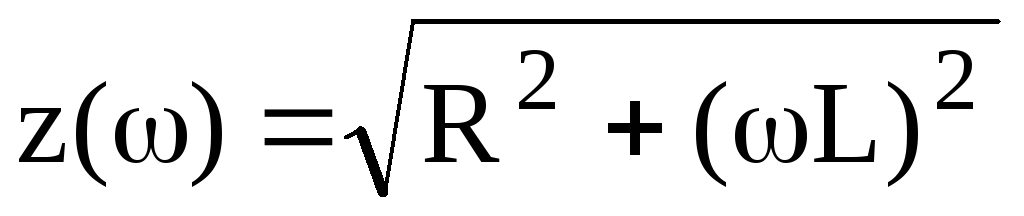 , z(0)=R; z()=.
, z(0)=R; z()=.
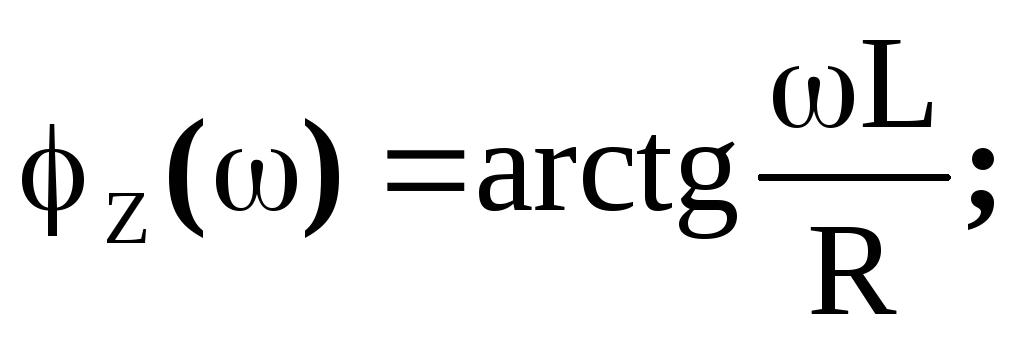 ,,z(0)=0 ,z()=.
,,z(0)=0 ,z()=.
П олучим выражения для KU(j), KU(), k(ω).
олучим выражения для KU(j), KU(), k(ω). 
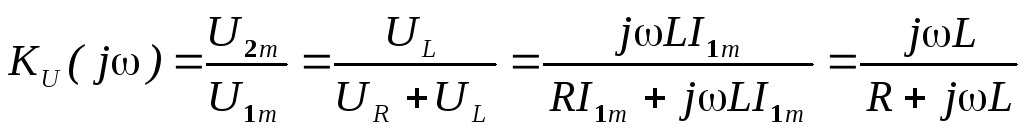
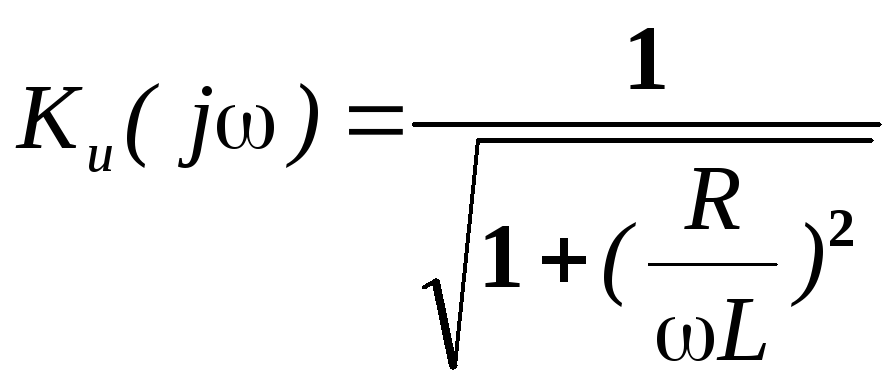 , Ku(0)=0, Ku()=1.
, Ku(0)=0, Ku()=1.
Графики зависимостей KU(), k(ω) приведены на рис.1.13.


Эта цепь, пропускающая сигналы высоких частот и подавляющая сигналы низких частот называется фильтром высоких частот (ФВЧ).
Определим граничную частоту. По определению 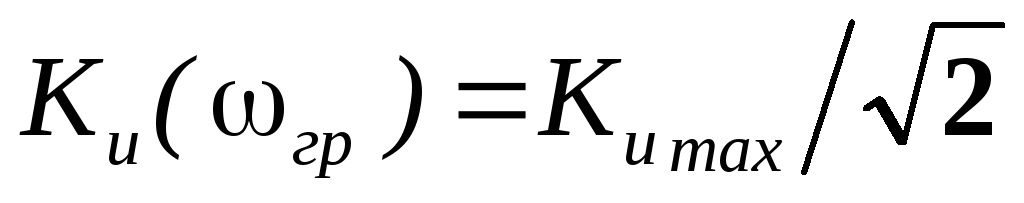 . Отсюда:
. Отсюда:
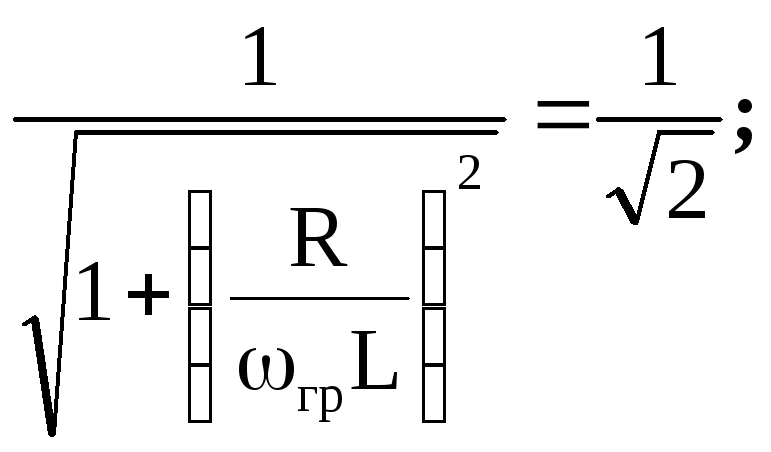
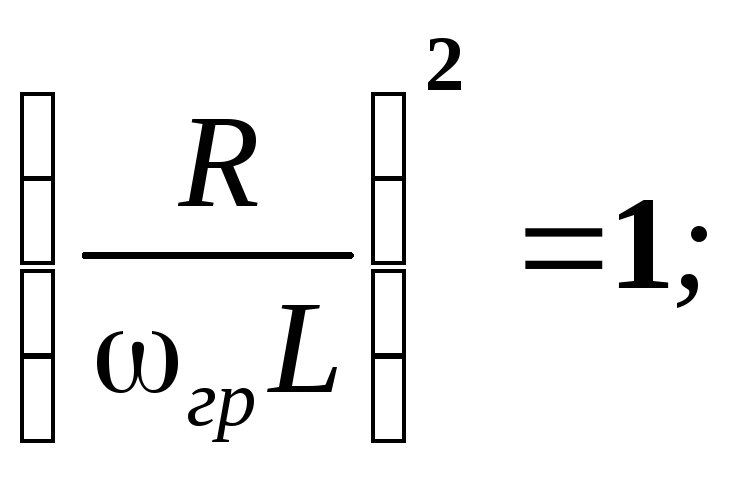
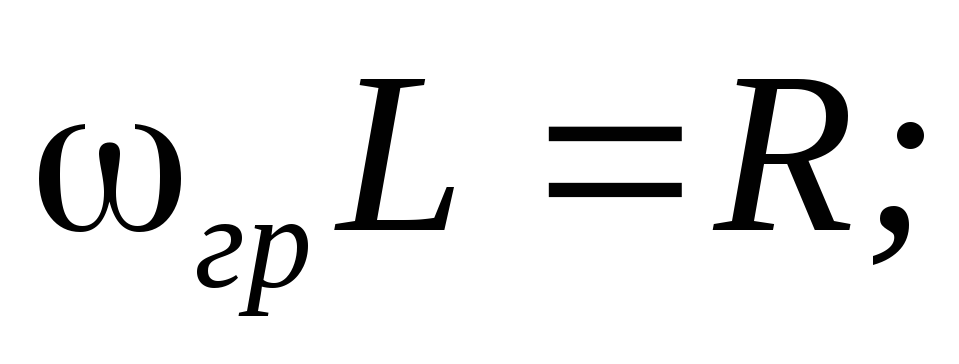
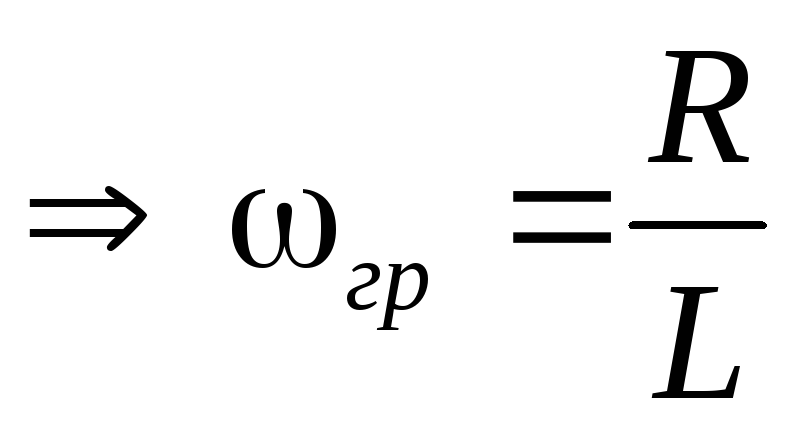 .
.
Пример 1.5. Для цепи (рис.1.14) определить комплексную функцию входного сопротивления Zвх(j), ее АЧХ — Zвх() и ФЧХ — 2().
Д ано: R1=1кОм R2=2кОм; R3=2кОм; C=1мкФ; L=10 -2 Гн.
ано: R1=1кОм R2=2кОм; R3=2кОм; C=1мкФ; L=10 -2 Гн.
Решение. Комплексную функцию входного сопротивления находим методом эквивалентных преобразований, перейдя к комплексной схеме замещения (рис.1.5).
На первом этапе преобразуем участок цепи, содержащий последовательное соединение элементов L и R3. Получим выражение для их комплексного сопротивления Z34=jL+R3.
На втором этапе преобразуем участок цепи, состоящий из параллельно соединенных элементов R2 и Z34. Получим 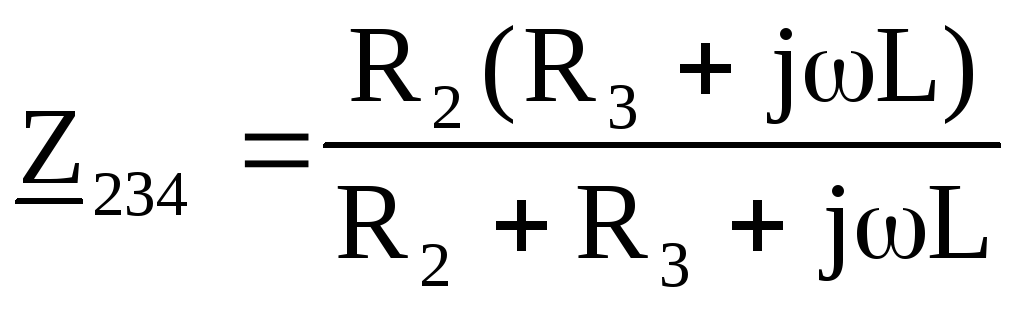 .
.
На третьем, заключительном, этапе преобразуем участок цепи, содержащий последовательное соединение ветви Z1, состоящей из последовательного соединения R1 и C и участка цепи с сопротивлением Z234. Получим
 .
.
Запишем полученное выражение в алгебраической форме:
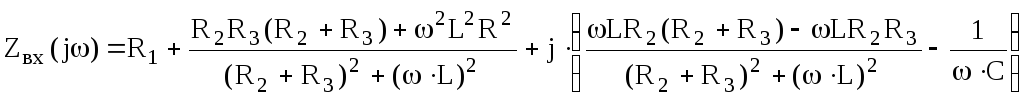 .
.
Отсюда выражения для АЧХ и ФЧХ имеют вид:
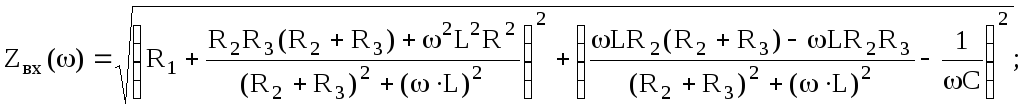
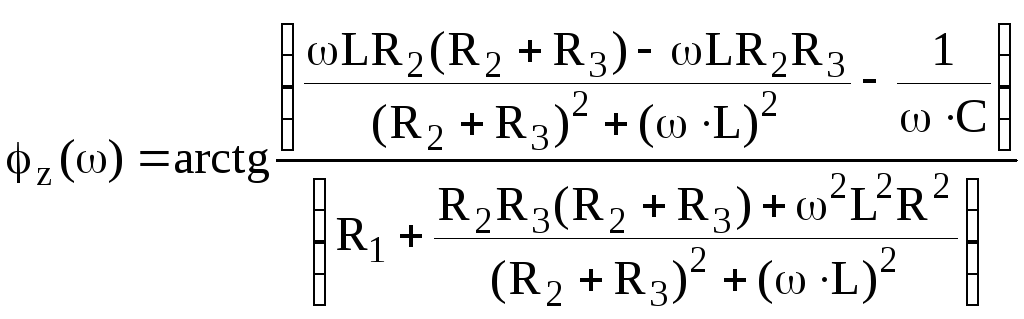 .
.
К ачественный анализ схемы показывает, что при=0, т.к. Xс= — входное сопротивление — равно бесконечности, а при , т.к. XC=0, XL=, входное сопротивление равно R1+R2. Это совпадает с расчетом по полученным выражениям, что подтверждает их правильность.
ачественный анализ схемы показывает, что при=0, т.к. Xс= — входное сопротивление — равно бесконечности, а при , т.к. XC=0, XL=, входное сопротивление равно R1+R2. Это совпадает с расчетом по полученным выражениям, что подтверждает их правильность.
Результаты расчета АЧХ и ФЧХ представлены на графиках (рис.1.15 и 1.16). При этом значение частоты взято в логарифмическом масштабе т.е. lg .
Пример 1.6. Для цепи (рис.1.14), используя метод контурных токов, вывести выражения для комплексной функции коэффициента передачи напряжений Ku(j) (его АЧХ — Ku() и ФЧХ — k()) и построить графики АЧХ и ФЧХ.
Решение. Топологический анализ показывает: число узлов nу=2, число ветвей nв=3. Отсюда число независимых контуров Nв=nу-nв+1=3-2+1=2. Выбираем направление обхода контуров, как правило, по часовой стрелке. Вводим обозначения и направления контурных токов 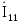 и
и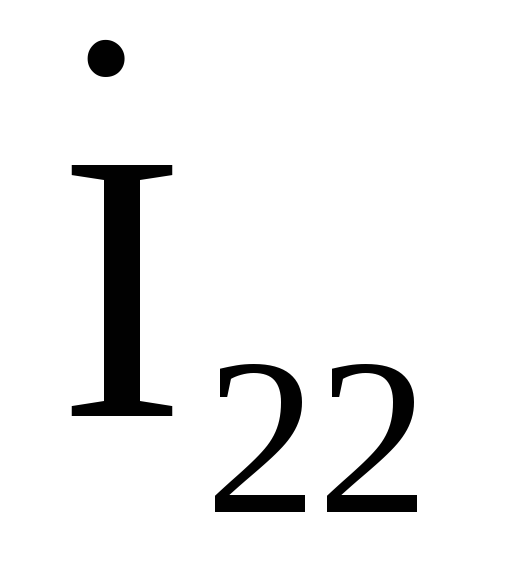 , как показано на рис. 1.14.
, как показано на рис. 1.14.
Для нахождения 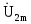 используя МКА необходимо найти ток
используя МКА необходимо найти ток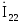 (
(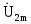 =R3
=R3 ). Система уравнений, составленная по методу контурных токов, имеет вид:
). Система уравнений, составленная по методу контурных токов, имеет вид:
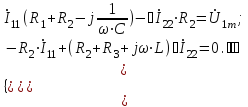
Решая систему по методу Крамера относительно тока 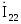 , получаем:
, получаем:
 .
.
Отсюда выражение для комплексного коэффициента передачи напряжения имеет вид:
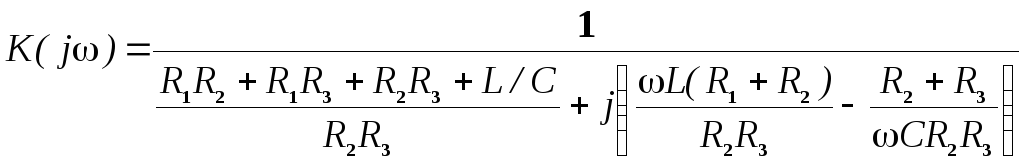 .
.
АЧХ и ФЧХ соответственно равны:
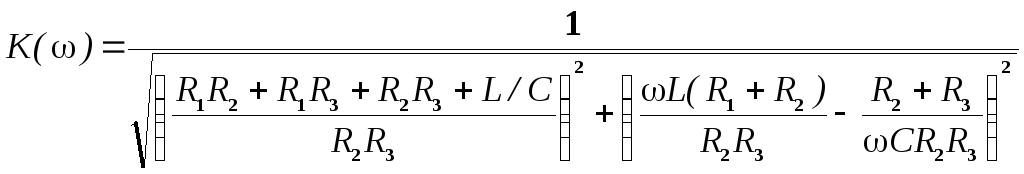 ;
;
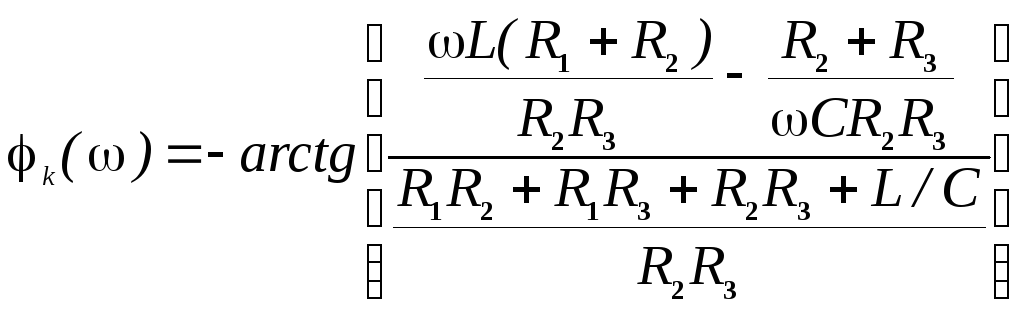 .
.
К ачественный анализ схемы показывает, что при=0, т. к. XC(), то U2m=0, т.е. Ku(0)=0. При =, XL(), а потому U2m=0, т.е. Ku()=0. Это ты совпадает с расчетом по полученным выражениям для АЧХ, что подтверждает правильность проведенных расчетов.
ачественный анализ схемы показывает, что при=0, т. к. XC(), то U2m=0, т.е. Ku(0)=0. При =, XL(), а потому U2m=0, т.е. Ku()=0. Это ты совпадает с расчетом по полученным выражениям для АЧХ, что подтверждает правильность проведенных расчетов.
Результаты расчета АЧХ и ФЧХ представлены на графиках (рис.1.17 и 1.18). При этом значения частоты взяты в логарифмическом масштабе, т.е. lg.
Пример 1.7. Решить пример 1.6 методом узловых потенциалов.
Решение. Схема содержит три узла (nу=3). Пронумеруем узлы и введем их обозначения (рис.1.14). Для нахождения U2m необходимо определить 2=U2m. Система уравнений, для нахождения 2, составленная по методу узловых потенциалов, имеет вид:
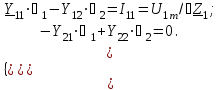
где 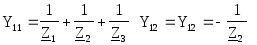 ,
,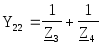 .
.
Решая эту систему относительно 2 по методу Крамера, получим:
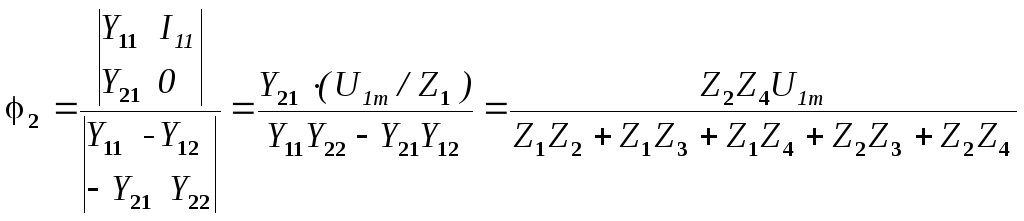 .
.
Отсюда, после подстановок, получим выражение для комплексного коэффициента передачи напряжения:
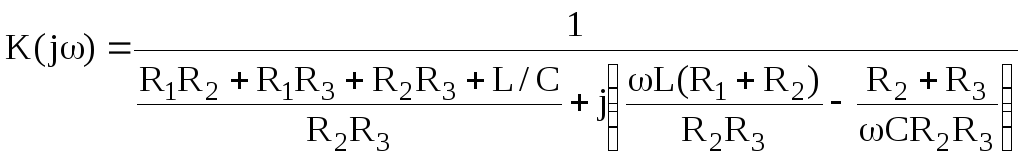 .
.
АЧХ и ФЧХ соответственно равны:
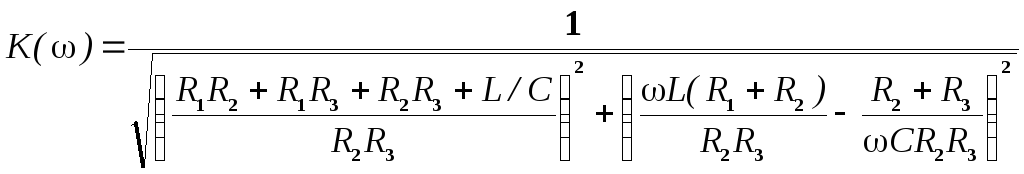 ,
,
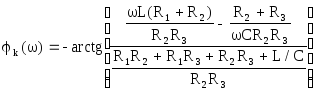 .
.
Сопоставляя результаты расчета в данном примере с результатами предыдущего примера, видим их полное совпадение. Это подтверждает правильность наших расчетов.

