На испытание поставлено 100 однотипных изделий. За 4000 час отказало 50 изделий. За интервал времени 4000—4100 час отказало еще 20 изделий. Требуется определить частоту и интенсивность отказов изделий в промежутке времени 4000—4100 час .
Ответ:  1/ час ;
1/ час ;  1/ час.
1/ час.
Используя данные задачи 1.4, определить вероятность безотказной работы и вероятность отказа изделий за первые 4 000 час .
Ответ: 
Используя данные задачи 1.4, вычислить вероятность безотказной работы и вероятность отказа изделий за время 4100 час .
Ответ: 
Расчет характеристик надежности Надежность информационных систем Типовые примеры и их решения
Методические указания по выполнению практических работ
по дисциплине «Надежность систем»
221400.62 «Управление качеством»
профиль «Управление качеством в производственно-технологических системах»
Практическая работа №1
Определение количественных характеристик надежности
по статистическим данным об отказах изделия
Вероятность безотказной работы по статистическим данным об отказах оценивается выражением
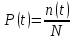 (1)
(1)
где n(t) число изделий, не отказавших к моменту времени t; Nчисло изделий, поставленных на испытания; Р(t) статистическая оценка вероятности безотказной работы изделия.
Для вероятности отказа по статистическим данным справедливо соотношение
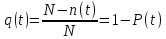 (2)
(2)
где N—n(t) число изделий, отказавших к моменту времени t; q(t) — статистическая оценка вероятности отказа изделия.
Частота отказов по статистическим данным об отказах определяется выражением
 (3)
(3)
где Δn(t) – число отказавших изделий на участке времени (t, t+Δt); f(t) – статистическая оценка частоты отказов изделия; Δt – интервал времени.
Интенсивность отказов по статистическим данным об отказах определяется формулой
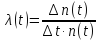 (4)
(4)
где n(t) – среднее число изделий, не отказавших к моменту времени t; Δn(t) – число отказавших изделий на участке времени (t, t+Δt); λ (t) – статистическая оценка интенсивности отказов изделия.
Среднее время безотказной работы изделия по статистическим данным оценивается выражением
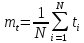 (5)
(5)
где ti – время безотказной работы i— го изделия; N – общее число изделий, поставленных на испытания; mt – статистическая оценка среднего времени безотказной работы изделия.
Для определения mt по формуле (5) необходимо знать моменты выхода из строя всех N изделий.
Задача 1. На испытание поставлено 1000 однотипных электронных ламп, за 3000 час. отказало 80 ламп. Требуется определить P(t), q(t) при t = 3000 час.
Решение. В данном случае N= 1000; n(t)=1000-80=920; N—n(t)=1000-920=80. По формулам (1) и (2) определяем
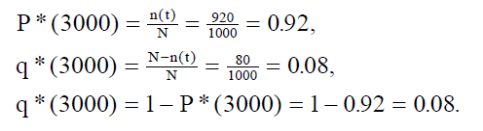
Задача 2. На испытание было поставлено 1000 однотипных ламп. За первые 3000 час. отказало 80 ламп, а за интервал времени 3000 — 4000 час. отказало еще 50 ламп. Требуется определить статистическую оценку частоты и интенсивности отказов электронных ламп в промежутке времени 3000 — 4000 час.
Решение. В данном случае N=1000; t=3000 час; Δt =1000 час; Δn(t)=50; n(t)=920.
По формулам (3) и (4) находим
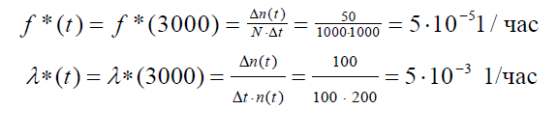
Задача 3. На испытание поставлено N = 400 изделий. За время t = 3000 час отказало 200 изделий, т.е. n(t) = 400-200=200.За интервал времени (t, t+Δt) , где Δt= 100 час, отказало 100 изделий, т.е. Δn(t)= 100. Требуется определить Р*(3000), P*(3100), f*(3000), λ*(3000).
Решение. По формуле (1) находим
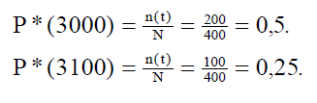
Используя формулы (3) и (4), получим

Задача4. На испытание поставлено 6 однотипных изделий. Получены следующие значения ti (ti время 6езотказной работы i— го изделия) : t1 =280 час; t2 = 350 час; t3 =400 час; t4 =320 час; t5 =380 час; t6 =330 час.
Определить статистическую оценку среднего времени безотказной работы изделия.
По word
Задание 1.7
На испытание поставлено 100 однотипных изделий. За 4000 час. отказало 50 изделий. За интервал времени 4000 — 4100 час. отказало ещё 20 изделий. Требуется определить f*(t),*(t) при t=4000 час.
Решаем по формуле :
 ,
,
 ,
,
f*(t)=f*(4000)=50/(100*4000)=125*10 -4 1/час
λ*(t)= λ*(4000)=50/(50*4000)=25*10 -4 1/час
Задача 3.11. Прибор состоит из n = 5 узлов. Надежность узлов характеризуется вероятностью безотказной работы в течение времени t , которая равна: P1(t)=0,98; P2(t)=0,99; P3(t)=0,998; P4(t)=0,975; P5(t)=0,985. Необходимо определить вероятность безотказной работы прибора.
Решение по формуле (3.1) Pc(t) =P1(t)*P2(t). Pn(t)=  где Рi(t) — вероятность безотказной работы i-го элемента за время t.
где Рi(t) — вероятность безотказной работы i-го элемента за время t.
Задание 4,4
Приемник состоит из трех. блоков: УВЧ, УПЧ и УНЧ. Интенсивности отказов этих блоков соответственно равны: 1= 4*10 -4 1/час; 2= 2,5*10 -4 1/час; 3= 3*10 -4 1/час. Требуется рассчитать вероятность безотказной работы приемника при t=100 час для следующих случаев:
а) резерв отсутствует;
б) имеется общее дублирование приемника в целом.
Решаем по формуле
 ;
;
Р1(100) = e — 4*0.0001*100 =0.04.
Р2(100) = e — 2.5*0.0001*100 =0.025.
Р3(100) = e — 3*0.0001*100 =0.03.
 = 1-(1-Pj ) m 2 =1-(1-3*10 -5 ) 2 =59*10 -5 1/час
= 1-(1-Pj ) m 2 =1-(1-3*10 -5 ) 2 =59*10 -5 1/час

