По данному натуральном nn вычислите сумму 1!+2!+3!+…+n!. В решении этой задачи можно использовать только один цикл. Пользоваться математической библиотекой math в этой задаче запрещено.
Комментарии
n = int(input())
partial_factorial = 1
partial_sum = 0
for i in range(1, n + 1):
partial_factorial *= i
partial_sum += partial_factorial
print(partial_sum)
res = 1
sum = 0
n = int(input())
for i in range(1, n + 1):
res *= i
sum += res
print(sum)
Добавить комментарий Отменить ответ
| ‹ | › | |||||
| Пн | Вт | Ср | Чт | Пт | Сб | Вс
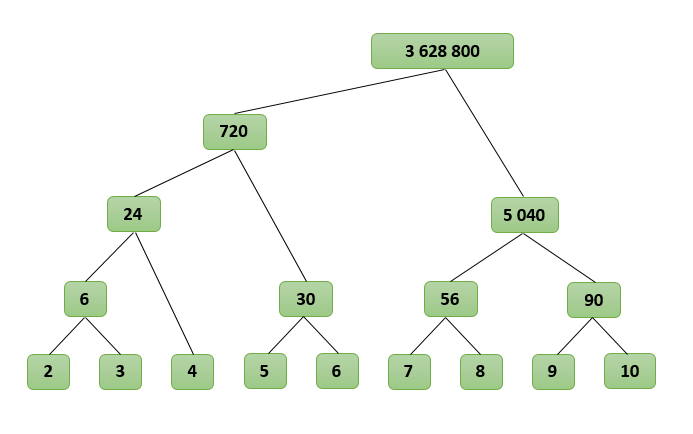
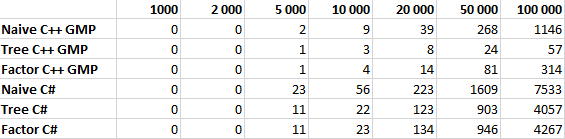
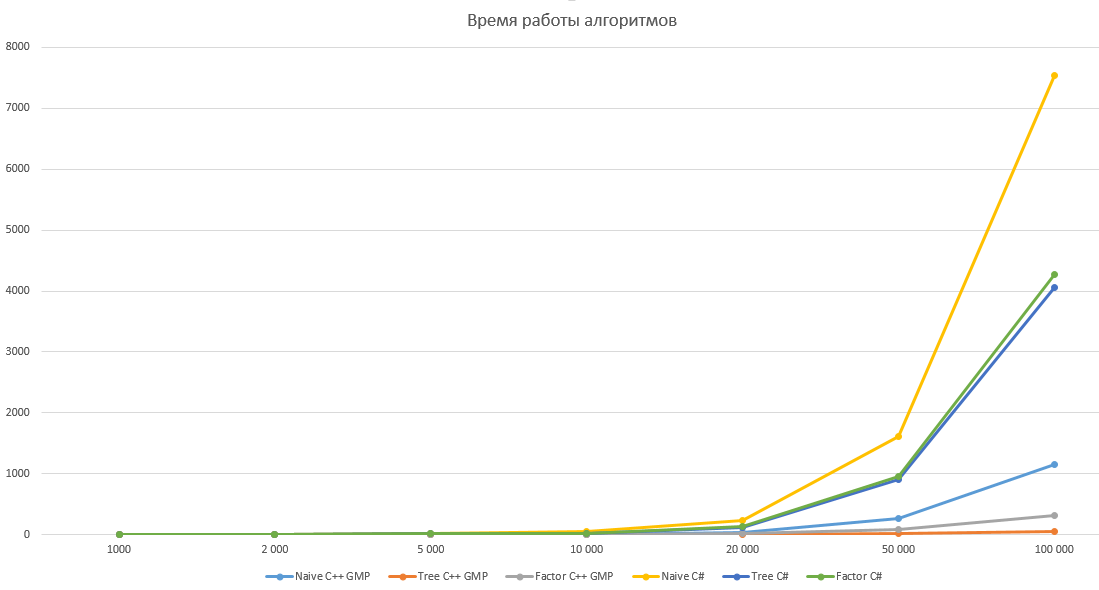
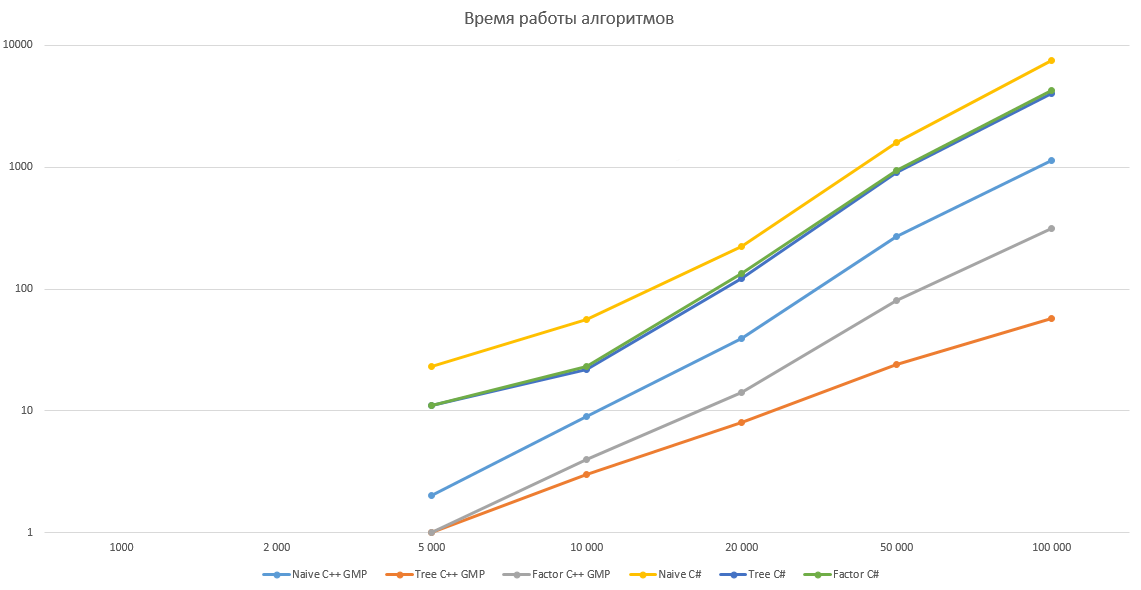
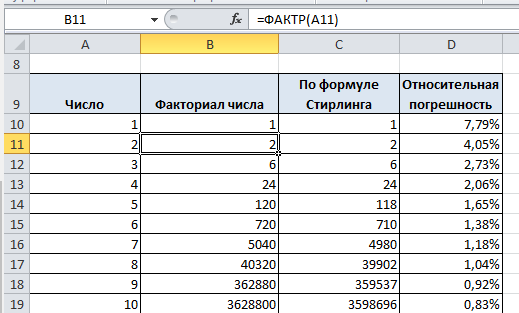
ЕГЭ на соточку для чайниковПрошу прощения, что так долго пропадал. Питошка вернулся, да еще и с группой в вконтакте, подписывайтесь. Помимо этого, на питошке откроется новая рубрика, в которой будут четкие объяснения всех заданий ЕГЭ и ОГЭ по информатике, внимательно прочитав которые, я уверен, вы улучшите свои баллы на экзамене 🙂 Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр. Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python. Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала: На моей машине эта реализация работает примерно 1,6 секунд для N=50 000. Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации. Алгоритм вычисления деревом Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины. Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N). Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10): P(2, 10) Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне Реализуем описанный алгоритм: Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации. Алгоритм вычисления факторизацией Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +… Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8. Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения: 10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800 Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена: Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000! Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью. Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах. График с линейной шкалой График с логарифмической шкалой Идеи и алгоритмы из комментариев Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них Исходные коды реализованных алгоритмов приведены под спойлерами В этой статье я расскажу о факториале, его свойствах и о том, как вычислить его значение с помощью Excel. Мы проверим, как точно вычисляет значение факториала формула Стирлинга и разберем решение типовых задач с факториалами, а на закуску — несколько видеороликов (и конечно расчетный файл эксель). Удачи! Что такое факториал?Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. Факториал определен только для целых неотрицательных чисел. $$n!=1cdot 2cdot 3 cdot . cdot (n-1) cdot n$$ По определению, считают, что $0!=1, 1!=1$. Далее: $$ 2!=1 cdot 2 = 2,\ 3!=1 cdot 2 cdot 3= 6,\ 4!=1 cdot 2 cdot 3cdot 4= 24,\ 5!=1 cdot 2 cdot 3cdot 4cdot 5= 120,\ . $$ Факториал растет невероятно быстро (недаром он обозначается восклицательным знаком!), существенно быстрее степенной $x^n$ или даже экспоненциальной функции $e^n$ (но медленее чем $e^$) Факториал широко применяется в комбинаторике — он равен числу всех перестановок $n$-элементного множества, а также входит в формулы для числа сочетаний и размещений. Факториал встречается в математическом анализе (чаще при разложениях функции в степенные ряды), а также в функциональном анализе и теории чисел. Формулы и свойства факториалаРекуррентная формула для факториала: Факториал связан с гамма-функцией по формуле: $n!= Gamma(n+1)$. Фактически, гамма-функция — обобщение понятия факториала на все положительные вещственные функции. Для любого натурального $n$ выполняется: $$ (n!)^2 ge n^n ge n! ge n. $$ Любопытная формула связывает факториал и производную степенной функции: Формула СтирлингаДля приближенного вычисления факториала применяют асимптотическую формулу Стирлинга: Обычно для расчетов берут только главный член: $$ n! approx sqrt <2pi n>left( frac Ниже вы увидите пример расчета факториала по обычной формуле и с помощью формулы Стирлинга, которая, как видно, дает вполне хорошее приближение (начиная с $n=9$ относительная погрешность уже меньше 1%). Расчет факториала в ЭксельДля нахождения факториала в Excel нужно использовать специальную функцию =ФАКТР($n$) , где $n$ — число, факториал которого нужно найти. Пример расчета и ввода формулы ниже на скриншоте, также вы можете скачать расчетный файл
Примеры задач с факториаломРассмотрим решение типовых задач. Пример 1. На полке стоят 8 дисков. Сколькими способами их можно расставить между собой? Решение. Требуется найти число всех перестановок 8 различных объектов, что вычисляется как раз как факториал: $$N=8!=1 cdot 2 cdot 3cdot 4cdot 5cdot 6cdot 7cdot 8=40320.$$ Пример 3. Упростить выражение Пример 4. Упростить дробь, содержащую факториал: Видео о факториалеНебольшое учебное видео про факториал — определение, свойства, как быстро растет, как вычислить в Excel по встроенной формуле и по приближенной формуле Стирлинга.
Расчетный файл из видео можно скачать Напоследок — насколько быстро растет факториал!
|