1. Пишущий элемент регистрирующего прибора совершает колебания по закону x = 2 sin π ( t – 0.4 ) (см). Определить амплитуду, период и начальную фазу колебания. Через какое время после начала отсчета пишущий элемент будет проходить положение равновесия?
Ответ: 2 см; 2 с; — 0.4 π; t = (k + 0.4) с.
2. При беге на средние дистанции колебания центра тяжести спортсмена можно рассматривать как гармонические. Считая наибольшее смещение центра тяжести тела спортсмена равным 10 см, определить максимальную скорость смещения его центра тяжести, если спортсмен делает 210 шагов в минуту.
3. Определить резонансную частоту ноги человека при маховых движениях, рассматривая ее как физический маятник с приведенной длиной 38.8 см.
4. Логарифмический декремент затухания маятника равен 0.02. Во сколько раз уменьшится амплитуда после 50 полных колебаний?
5. Определить разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии 20 см друг от друга. Скорость пульсовой волны считать равной 10 м/с, а колебания сердца – гармоническими с частотой 1.2 Гц.
6. Определить скорость движения передней стенки желудочка сердца в сторону груди, если при эхолокации ультразвуком частотой 800 кГц отраженный сигнал воспринимался на частоте 800.21 кГц. Скорость ультразвука принять равной 1540 м/с.
7. Шум мотора грузового автомобиля с уровнем интенсивности 80 дБ воспринимается в закрытом помещении, как шум с уровнем интенсивности звука 50 дБ. Найти отношение интенсивностей звука на улице и в комнате.
8. Определить интенсивность сердечных тонов у входа в воронку стетоскопа диаметром 6 см, если на барабанную перепонку площадью 70 мм 2 попадает 74 % звуковой энергии при интенсивности 10 -15 Вт/см 2 .
Ответ: ≈ 3.3 ∙ 10 -17 Вт/см 2 .
9. Для большинства людей с нормальным слухом изменение громкости звука частотой 1000 Гц ощущается при изменении интенсивности звука на 26 %. Какому интервалу громкости соответствует указанное изменение интенсивности звука?
10. Рассматривая биения сердца как гармонические колебания, определить разность фаз в пульсовой волне между двумя точками артерии, расположенными на расстоянии 25 см друг от друга (локтевая ямка и нижняя треть предплечья). Скорость пульсовой волны считать равной 8 м/с, а частоту биений сердца – 70 ударов в минуту.
Дата добавления: 2015-09-04 ; просмотров: 1267 . Нарушение авторских прав
Конечным элементом технической схемы, изображенной на рис. 17.1, является измерительное (контролирующее) устройство, отображающее или регистрирующее медико-биологическую информацию.
Под устройством отображения понимают устройство, которое временно представляет информацию, при появлении новой информации прежняя информация бесследно исчезает. Такими являются, в частности, стрелочные приборы: амперметр, вольтметр и др. Стрелочный амперметр, например, показывает силу тока в данный момент и не фиксирует ее. При изменении силы тока в цепи информация о прежнем значении безвозвратно утрачивается. Для запоминания информации, отображаемой такими устройствами, необходимо специально ее фиксировать, что, например, и делают студенты в физической лаборатории, снимая показания приборов. Медико-биологическое применение устройств отображения достаточно мало: электротермометр сопротивления, частотомер пульса и др.
Значительно большее распространение в медицинской электронике получили регистрирующие приборы, которые фиксируют информацию на каком-либо носителе. Это позволяет документировать, хранить, многократно использовать, обрабатывать и анализировать полученную медико-биологическую информацию.
Отображающие и регистрирующие приборы подразделяют на аналоговые — непрерывные, дискретные и комбинированные, сочетающие возможности аналоговых и дискретных.
Рассмотрим подробнее наиболее распространенные в практике медико-биологических исследований аналоговые регистрирующие устройства. Некоторые из них называют также самопишущими приборами или самописцами.
В медицине, биологии и физиологии в основном используются следующие способы регистрации информации на носителе: а) нанесение слоя вещества (красителя): чернильно-перьевая и струеписная системы; б) изменение состояния вещества носителя: фоторегистрация, электрохимическая, электрофотографическая (ксерография) и магнитная запись; в) снятие слоя вещества с носителя: закопченная поверхность, тепловая запись.
Простейшим самописцем, находящим и сегодня применение в физиологическом эксперименте, является кимограф (рис. 17.8), работающий от заведенной пружины, или электрокимограф, равномерное вращение барабана которого осуществляется электродвигателем.
Идея кимографа — равномерное вращение или перемещение поверхности носителя — сохраняется в подавляющем большинстве современных аналоговых регистрирующих приборов, фиксирующих временную зависимость исследуемой величины. Смещение у писчика или светового пятна, пропорциональное регистрируемой величине, является ординатой полученного графика (рис. 17.9). Равномерное перемещение носителя (бумага, фотопленка) означает, что абсцисса прямо пропорциональна времени t. В результате полученная кривая отражает зависимость у = f(t).
Самопишущие приборы, используемые в медицинской аппаратуре, преобразуют электрический сигнал в механическое перемещение. Физически они являются гальванометрами — высокочувствительными электроизмерительными приборами, реагирующими на достаточно малую силу тока. В этих приборах ток, проходящий по катушкам, проволочной рамке или по петле, взаимодействует с магнитным полем постоянного магнита. В результате этого взаимодействия подвижная часть (магнит, проволочная рамка или части петли) отклоняется пропорционально силе тока, т. е. пропорционально электрическому сигналу.
 |
С подвижной частью соединен пишущий элемент, оставляющий след на движущемся носителе записи: специальное капиллярное перо, либо стеклянный капилляр с соплом в струйном самописце, либо зеркальце, отражающее луч света, или что-то другое.
В качестве примера на рис. 17.10 схематически изображен струйный самописец. Здесь 1 — электромагнит, через обмотки которого проходит регистрируемый электрический сигнал; 2 — постоянный магнит в форме цилиндра, он жестко связан со стеклянным капилляром 3. Из сопла капилляра 4 под давлением вылетают чернила, оставляя след у, пропорциональный отклонению постоянного магнита и, следовательно, силе тока в электромагните.
Важной характеристикой самописца является диапазон частот колебаний, которые они успевают регистрировать. Чем больше инерция подвижной части самописца, тем больше запаздывание регистрации относительно истинного изменения регистрируемой величины и тем хуже характеристика прибора.
В самопишущих устройствах наряду с обычными погрешностями измерительных приборов возникают также погрешности, обусловленные записью.
Причинами погрешности записи могут быть неточность работы механизма перемещения бумаги или фотопленки, запаздывание, вызванное инерцией пишущей системы прибора, изменение размеров бумаги под влиянием влажности воздуха, неточность отметки времени и др.
Кроме однокоординатных самописцев, фиксирующих временную зависимость, в исследовательской практике получили распространение двухкоординатные самописцы. На рис. 17.11 показан внешний вид такого самописца. При регистрации поперечная рейка перемещается поступательно, ее смещение пропорционально одному из подаваемых сигналов — параметров х. Вдоль рейки пропорционально изменению второго параметра у перемещается каретка с писчиком. В результате писчик совершает сложное движение и оставляет на бумаге график функции у = f(x).
 |
Наряду с аналоговыми регистрирующими устройствами в медицинской практике для
фиксирования информации используются и такие безынерционные комбинированные устройства, как электронно-лучевые трубки (см. § 18.8).
Так, например, в портативном вектор-кардиоскопе (см. рис. 17.14) электронно-лучевая трубка является основным элементом, который отображает, а при дополнительном фотографировании и регистрирует электро- и вектор-кардиограммы.
Электронно-лучевая трубка относится к группе комбинированных устройств, так как может отображать (при дополнительном фотографировании — регистрировать) выходную информацию не только в аналоговой, но и в дискретной форме (цифры, буквы).
Во второй главе показано, что вектор  горизонтальной составляющей угловой скорости вращения Земли может быть использован для получения навигационной информации.
горизонтальной составляющей угловой скорости вращения Земли может быть использован для получения навигационной информации.
Во-первых, данный вектор горизонтален, находится в плоскости меридиана и является касательным к нему. Очевидно, что определение направления этого вектора дает возможность найти плоскость меридиана. Данную задачу и решают гирокомпасы.
Во-вторых, измерение модуля вектора ω1 позволяет определить широту места. Такое определение выполняют некоторые типы инерциальных навигационных систем. В них измеряется величина ω1 = Ω1 (Ω1 — приборное или измеренное значение горизонтальной составляющей угловой скорости вращения Земли). Отсюда Ω1 = ω  ♀ cos φ. Полная величина угловой скорости вращения Земли известна, тогда φ = arccos Ω1/ ω♀.
♀ cos φ. Полная величина угловой скорости вращения Земли известна, тогда φ = arccos Ω1/ ω♀.
Рассмотрим более подробно принцип работы гирокомпасов с непосредственным управлением.
Смещение центра тяжести чувствительного элемента гирокомпаса относительно центра подвеса — это первое условие превращения свободного гироскопа в гирокомпас. В параграфе 2.4.3 рассмотрено движение такого гироскопа на Земле. Для более подробного анализа реализации этого условия необходимо составить уравнения движения чувствительного элемента в горизонтной системе координат. Для этого воспользуемся уравнениями движения свободного гироскопа (2.1). Поскольку главная ось чувствительного элемента гирокомпаса всегда близка к плоскостям горизонта и меридиана, то углы α и β малы. Тогда tg β ≈ О, sin α ≈ α. Теперь уравнения примут вид
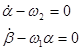 ; (3.3)
; (3.3)
Как рассматривалось в параграфе 2.4.3, вследствие вращения Земли гироскоп в горизонтной системе координат видимым образом движется в азимуте с угловой скоростью  , а по высоте — с угловой скоростью
, а по высоте — с угловой скоростью 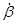 . С появлением угла β, то есть с отклонением центра тяжести от вертикальной линии, проходящей через центр подвеса чувствительного элемента, появляется плечо (рис. 3.3)
. С появлением угла β, то есть с отклонением центра тяжести от вертикальной линии, проходящей через центр подвеса чувствительного элемента, появляется плечо (рис. 3.3)
DG = a sin β ≈ а β .
С появлением плеча возникает момент силы тяжести Ly = В β (см.(2.12)), называемый маятниковым моментом. Последнее обстоятельство приводит к прецессии гироскопа к западу:
ωpz =— 
Так как угол β мал, cos β ≈ 1, то проекция полученной угловой скорости на вертикаль равна ωpz.
 |
Угловая скорость прецессии в азимуте войдет в первое уравнение системы (3.3)
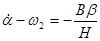
На движение гироскопа по высоте никакого дополнительного влияния не возникло. Окончательно уравнения примут вид
 ,
,
 (3.4)
(3.4)
Получены дифференциальные уравнения движения чувствительного элемента в горизонтной системе координат. Они с достаточной степенью точности характеризуют это движение как в азимуте, так и по высоте.
Такой же результат дает способ Кудревича, рассмотренный в параграфе 2.2. Просуммировав гироскопические моменты Н  , Hω2 и момент силы тяжести, приложенные по оси у, получим первое уравнение, а сумма гироскопических моментов по оси z дает второе уравнение системы (3.4). Малые члены уравнений исключены из рассмотрения заранее для упрощения преобразований.
, Hω2 и момент силы тяжести, приложенные по оси у, получим первое уравнение, а сумма гироскопических моментов по оси z дает второе уравнение системы (3.4). Малые члены уравнений исключены из рассмотрения заранее для упрощения преобразований.
Уравнения описывают незатухающие колебания гирокомпаса, характер и физический смысл которых изложен в параграфе 2.4.3.
Незатухающие колебания совершаются у положения равновесия, которое займет ось х чувствительного элемента, когда прекратится движение, то есть при  = 0 и
= 0 и 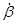 = 0. Подставив эти значения в уравнения (3.4), получим их частные решения:
= 0. Подставив эти значения в уравнения (3.4), получим их частные решения:
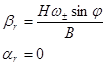 (3.5)
(3.5)
Данные уравнения характеризуют положение равновесия главной оси гирокомпаса.
1. Главная ось гироскопа находится в плоскости меридиана. Она приподнята над плоскостью горизонта на угол βr, что приводит к появлению момента Вβr. Наличие этого момента обеспечивает прецессию оси х гирокомпаса вслед за уходящим к западу меридианом:
ωpz =— 
2. Угол βr зависит от широты.
Для нахождения общего решения уравнений движения (3.4) необходимо разделить переменные. Продифференцируем первое уравнение:

Из второго уравнения подставим значение 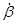 и после преобразования получим
и после преобразования получим
 (3.6)
(3.6)
 (3.7)
(3.7)
здесь ω — круговая частота незатухающих колебаний. Причем ω =В/Н и ω = ω♀ cos φ. Отсюда найдем период незатухающих колебаний как величину, обратно пропорциональную_частоте:
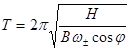 (3.8)
(3.8)
Из анализа уравнений следует:
1. Период незатухающих колебаний зависит от широты. На экваторе он минимален, на полюсе — стремится к бесконечности, что происходит вследствие потери гирокомпасом избирательности к меридиану.
2. Период Т зависит от параметров гирокомпас Н и В. Это дает возможность его регулировать.
Гирокомпас представляет собой автоматическую систему. Для ее оценки с точки зрения основ автоматики произведем линейное преобразование уравнения (3.6), считая  = λ. Следовательно,
= λ. Следовательно,
Выражение (3.9) является характеристическим уравнением и имеет мнимые корни
где i =  .
.
В соответствии с критериями устойчивости Гурвица система неустойчива, если корни характеристического уравнения мнимые. Переходный процесс имеет гармонический характер. Следовательно, гирокомпас совершает гармонические незатухающие колебания.
Общее решение уравнения (3.6) имеет вид
Для начальных условий (t = 0) последний член уравнения равен нулю, а угол отклонения в азимуте максимален и равен α, то есть С1= α. Тогда
Из анализа уравнения (3.11) можно заключить, что гирокомпас совершает незатухающие колебания с амплитудой, равной начальному отклонению главной оси чувствительного элемента от плоскости истинного меридиана. Величиной C2 пренебрегаем ввиду ее незначительности.
Для нахождения закона движения главной оси гироскопа по высоте продифференцируем уравнение (3.11):
 = —α ωsin ω t.
= —α ωsin ω t.
Подставив это значение в первое уравнение системы (3.4), получим

Для упрощения данного выражения произведем замену
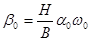
Здесь все составляющие постоянны. Последний член уравнения равен βr (см.(3.5)). После замены выражение примет вид

Уравнение (3.11) можно представить в виде

Воспользовавшись теоремой Пифагора, найдем текущее значение конца вектора  чувствительного элемента для любого момента времени (рис. 3.3)
чувствительного элемента для любого момента времени (рис. 3.3)
 (3.12)
(3.12)
Это выражение является уравнением эллипса с центром αr = 0, β = βr и с полуосями: большой α, малой β. Это и есть траектория движения главной оси гироскопа. Анализ этого движения описан в параграфе 2.4.3.
Итак: выполнено первое условие превращения свободного гироскопа в гирокомпас. Хотя таким прибором пользоваться еще нельзя, так как он совершает незатухающие колебания, но эти колебания происходят вокруг известного направления — истинного меридиана, а говоря строже — направления вектора горизонтальной составляющей угловой скорости вращения Земли.
Последнее уточнение рассмотрим подробнее. Маятниковый момент создается благодаря смещению центра тяжести гироскопа относительно центра подвеса, а также вследствие вращения Земли. В положении равновесия центр тяжести чувствительного элемента вращается в инерциальном пространстве вокруг вектора ω1, совершая один оборот в сутки. Именно к его направлению и приходит главная ось чувствительного элемента. В свою очередь этот вектор находится в плоскости истинного меридиана. Следовательно, в частном случае, а именно — при неподвижном основании, когда гирокомпас участвует только в одном вращении — вращении Земли, он приходит в плоскость истинного меридиана.
Обратимся ко второму уравнению системы (3.4). Домножим все его члены на величину Н. С учетом вышесказанного второй член этого уравнения является моментом
который характеризует реакцию гироскопа с пониженным центром тяжести на его отклонение в азимуте от направления вектора ω1 (то есть от плоскости истинного меридиана). Данный момент является гироскопическим моментом и возникает при движении гироскопа по высоте 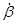 (рис.3.3). Движение по высоте вследствие вращения Земли происходит только в случае, когда α ≠ 0. Таким образом, Rz является направляющим моментом гирокомпаса. Анализ уравнения (3.13) позволяет сделать следующие выводы:
(рис.3.3). Движение по высоте вследствие вращения Земли происходит только в случае, когда α ≠ 0. Таким образом, Rz является направляющим моментом гирокомпаса. Анализ уравнения (3.13) позволяет сделать следующие выводы:
1. Направляющий момент может возникать только при вращении Земли. Это обязательное условие превращения свободного гироскопа в гирокомпас. На любой планете, не имеющей вращения, чувствительный элемент занимал бы неопределенное положение (ω♀ = 0, Rz = 0).
2. Гирокомпас занимает также неопределенное положение и на полюсе (cos 90° = 0, Rz: = 0), вследствие потери направляющего момента. Фактически гирокомпас теряет избирательность к меридиану в широтах выше 75  85°, когда Rz становится малым и соизмеримым с вредными моментами. Гирокомпасы, установленные на подводной лодке "Ленинский комсомолец", совершившей плавание на северный полюс в 1962 г., по техническим условиям должны были работать до широты 85°. Фактически они потеряли чувствительность к меридиану в широте 86,5°. Это отмечено в воспоминаниях бывшего командира этой лодки Жильцова. Для гирокомпаса "Курс-4" и его модификаций предельная рабочая широта составляет 75°.
85°, когда Rz становится малым и соизмеримым с вредными моментами. Гирокомпасы, установленные на подводной лодке "Ленинский комсомолец", совершившей плавание на северный полюс в 1962 г., по техническим условиям должны были работать до широты 85°. Фактически они потеряли чувствительность к меридиану в широте 86,5°. Это отмечено в воспоминаниях бывшего командира этой лодки Жильцова. Для гирокомпаса "Курс-4" и его модификаций предельная рабочая широта составляет 75°.
3. Направляющий момент обращается в ноль, когда гирокомпас в меридиане (α = 0, Rz = 0).
Итак, для превращения свободного гироскопа в гирокомпас в условиях вращающейся Земли нужно "связать" с нею гироскоп. Связь гироскопа с Землей осуществляется реализацией конструктивных решений. Для гирокомпаса "Курс-4" таким решением является снижение центра тяжести чувствительного элемента относительно центра подвеса. Это приводит к возникновению незатухающих колебаний, теоретический анализ которых приведен в настоящем параграфе, а графический — в параграфе 2.4.3.
Однако такой прибор еще не является гирокомпасом. Необходимо превратить его незатухающие колебания в затухающие. Для этой цели служит масляный успокоитель (жидкостный демпфер). Введение дополнительного устройства, масляного успокоителя, использующего в своей работе также силу тяжести, — это выполнение второго условия превращения свободного гироскопа в гирокомпас.
Затухающие колебания
В любых автоматических системах гашение механических колебаний производится с помощью момента, сдвинутого от основного момента либо по фазе (по времени), либо в пространстве на 90°. В первом случае оба момента прикладываются по одной оси, во втором — по разным.

