Запускаем цикл с параметром For для нахождения нулевых элементов главной диагонали после чего осуществляе перестановку элементов. Далее перемножаем все элементы главной диагонали. Затем при помощи оператора условия if then else, проверяем, что если определитель равен 0 то обратной матрицы не существует. После чего осуществляем операции с матрицей.
Надо написать программу в паскале для поиска определителя матрицы по такому алгоритму:
1. В 1-ом столбце ищем максимальный по модулю эл-т и запоминаем номер строки
2. Если этот эл-т равен 0, то и определитель равен нулю
3. Если номер строки не равен 1, то меняем эту строку с 1-ой и умножаем определитель на -1
4. Делим 1 строку на эл-т [1;1] и умножаем определитель на эл-т [1;1]
5. Из j-ого столбца (от 2 до размерности) вычитаем 1-ый столбец, умноженный на [1;j]
Все это делаем (размерность матрицы-1) раз
умножаем определитель на последний эл-т в матрице.
Я составила вот такую программу:
Type mas = array [1..10, 1..10] of real;
Var n: Integer;
d: real;
a: mas;
Procedure vvod (Var A: Integer);
Var rk: Integer;
begin
<$I->
repeat
Writeln (‘Vvedite razmernost matrici’);
Readln (a);
rk:=ioresult;
if (rk<>0) or (A 10) then
Writeln (‘error’)
until (rk=0) and (A>0) and (A abs (max)) then begin
max:=a[i, j];
k:=i
end;
if max=0 then
det:=0
else begin
if (k<>j) then begin
det:=det*(-1);
for i:=j to n do begin
b:=a[j, i];
a[j, i]:=a[k, i];
a[k, i]:=b end;
end;
for i:=j to n do
a[j, i]:= a[j, i]/a[j, j];
det:= det*a[j, j];
for i:=j+1 to n do begin
for c:=1 to n do
a[c, i]:= a[c, i] — a[c, j]*a[i, j];
end;
end;
j:=j+1;
end;
det:=det*a[n, n];
end;
Procedure Vivod (m: mas; n: integer);
Var i, j: Integer;
begin
For i:=1 to n do
begin
for j:=1 to n do
Write (m[i, j]:7:3, ‘ ‘);
Writeln;
end;
end;
begin
vvod (n);
Zap (a, n);
Vivod (a, n);
Readln;
deter (a, n, d);
Readln;
Writeln (‘Opredelitel matrici ‘, d:5:3);
Readln;
end.
С 5-ым шагом выходит как-то не получается. Помогите найти в чем ошибка
Пример седьмой. Вычисление определителя матрицы.
Из свойств определителя известно, что определитель матрицы порядка N может быть представлен в виде суммы N определителей N-1 порядка (разложение по строке или столбцу). Предположим мы раскладываем по первому столбцу. При этом определитель равен сумме произведений элементов этого столбца на минор данного элемента матрицы и на -1 в степени суммы индексов элемента. Минор элемента а[i,j] матрицы — это определитель матрицы, полученной вычеркиванием i-той строки и j-того столбца. 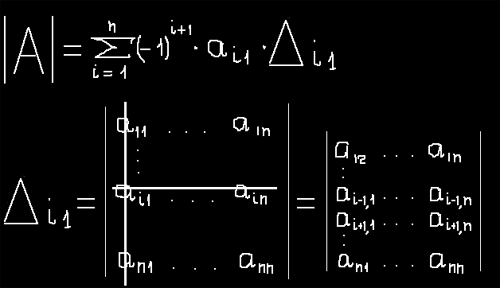
Таким образом можно воспользоваться рекурсией и написав одну простую процедуру вычислять определители матрицы любого порядка.
const n=4; < размерность матрицы >
type matr=array[1..n,1..n] of longint;
var a,b:matr;
i,j,dt:longint;
procedure PrintMatr(m:matr;n:integer);
< процедура вывода матрицы на экран >
var i,j:integer;
begin
for i:=1 to n do
begin
for j:=1 to n do
write(m[i,j]:3);
writeln;
end;
end;
procedure GetMatr(a:matr; var b:matr; m,i,j:integer);
< Вычеркивание из матрицы строки и столбца >
var ki,kj,di,dj:integer;
begin
di:=0;
for ki:=1 to m-1 do
begin
if (ki=i) then di:=1;
dj:=0;
for kj:=1 to m-1 do
begin
if (kj=j) then dj:=1;
b[ki,kj]:=a[ki+di,kj+dj];
end;
end;
end;
Function Determinant(a:matr;n:integer):longint;
< Вычисление определителя матрицы >
var i,j,d,k:longint;
b:matr;
begin
d:=0; k:=1;
if (n 2 >
for i:=1 to n do
begin
GetMatr(a,b,n,i,1);
PrintMatr(b,n-1);>
d:=d+k*a[i,1]*Determinant(b,n-1);
k:=-k;
end;
Determinant:=d;
end;
begin
< Заполнение матрицы случайными числами >
randomize;
for i:=1 to n do
for j:=1 to n do
a[i,j]:=random(5);
< Печать исходной матрицы >
PrintMatr(a,n);
< Вычисление и вывод определителя >
dt:=Determinant(a,n);
writeln(‘=========’);
writeln(‘Determinant=’,dt);
end.

