Кумулятивная кривая (кривая накопленных относительных частот) строится следующим образом. Если вариационный ряд дискретный, то в прямоугольной системе координат строят точки (xi,i нак ) и соединяют их отрезками; где
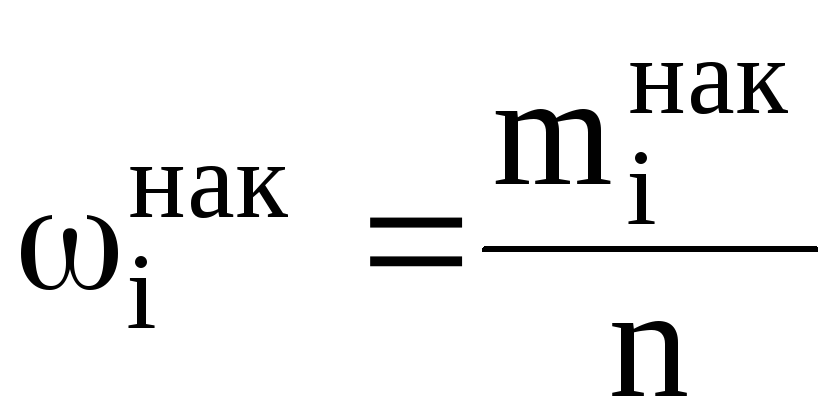

 , (2.4)
, (2.4)
причем mi нак — накопленная частота, т.е. сумма частот вариант x, удовлетворяющих условию x xi. Для вариационного ряда
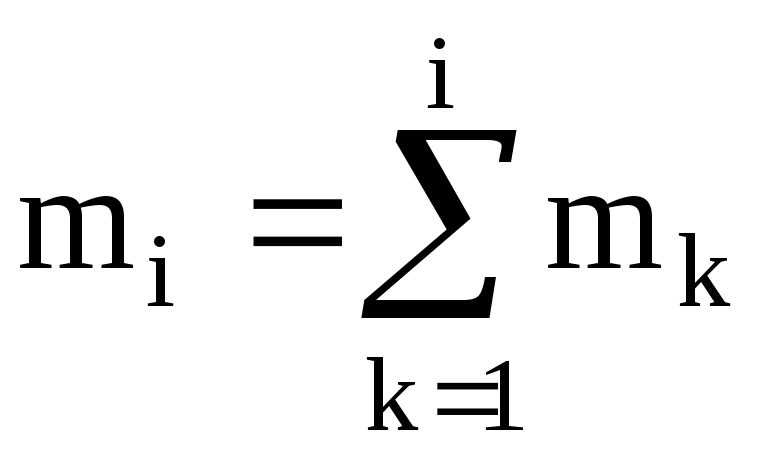 , (2.5)
, (2.5)
Пример 5. Построить комуляту для ряда из табл.2.1. Значения накопленных частот представлены в табл.2.5., а комулята на рис.2.3.
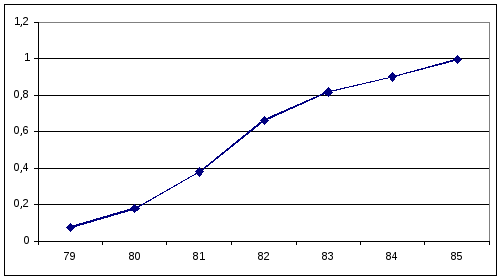
Рис.2.3. Кумулятивная кривая
Если вариационный ряд интервальный, то по оси абсцисс откладывают интервалы. Верхним границам интервалов соответствуют накопленные частоты, нежней границе первого интервала — накопленная частота, равная нулю. Значения накопленных частот для интервального ряда из табл.2.2. представлены в табл.2.6., а комулята представлена на рис. 2.4.
Накопленные относительные частоты

Рис.1.4. Кумулятивная кривая для интервального ряда
Таким образом, полигон и гистограмма являются приближением к графику дифференциальной функции распределения случайной величины X, а комулята — интегральной функции распределения для X.
Точечные оценки параметров распределения
Законы распределения случайной величины полностью ее описывают, однако на практике закон распределения не всегда может быть найден, кроме этого при решении многих практических задач нет необходимости характеризовать случайную величину исчерпывающим образом, а достаточно указать только отдельные числовые характеристики, которые определяют существенные черты распределения случайной величины.
Характеристики распределения случайной величины X оценивают посредством характеристик выборки (характеристик вариационных рядов), которые при увеличении n сходятся по вероятности к соответствующим характеристикам X, и при достаточно большом n могут быть приближенно равными им [1 — 5].
К основным несмещенным и состоятельным оценкам [1 — 3] относятся характеристики вариационных рядов: выборочная средняя — x, исправленная дисперсия — S *2 , среднее квадратичное отклонение — S * , коэффициент вариации — V, размах вариации — R, асимметрия — As , эксцесс — Ex , которые определяются по следующим формулам.
Средняя арифметическая — x
 (2.6)
(2.6)
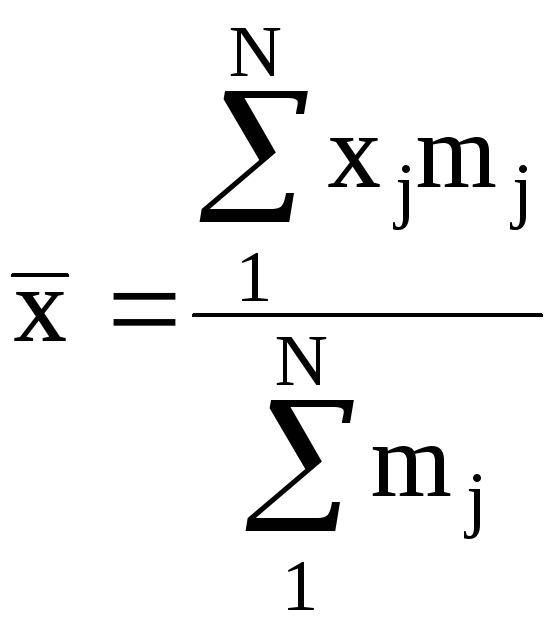 (2.7)
(2.7)
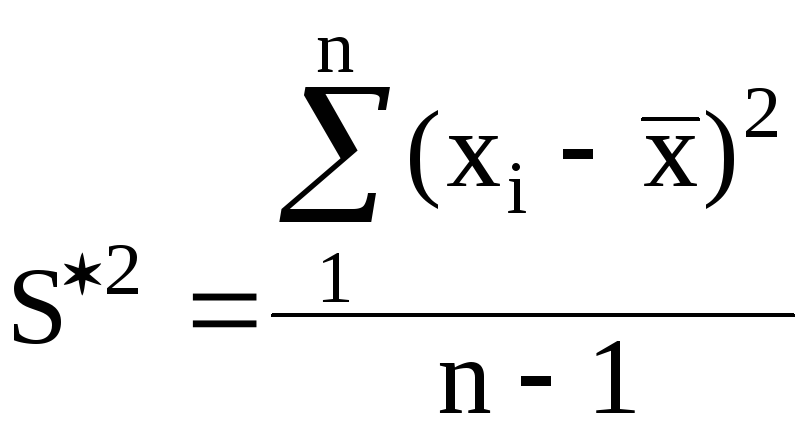 (2.8)
(2.8)
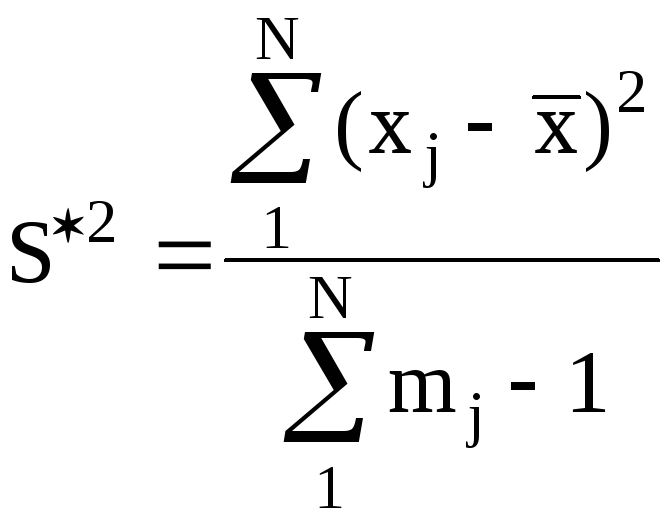 (2.9)
(2.9)
Среднее квадратичное отклонение (эмпирический стандарт) — S *
S * =  =
= 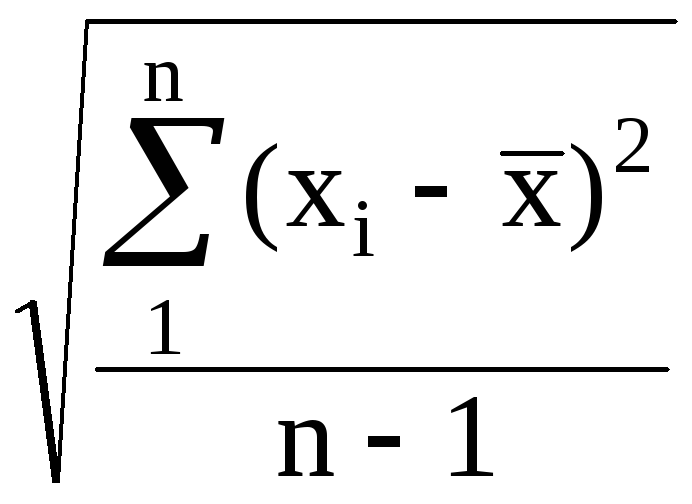 (2.10)
(2.10)
S * = 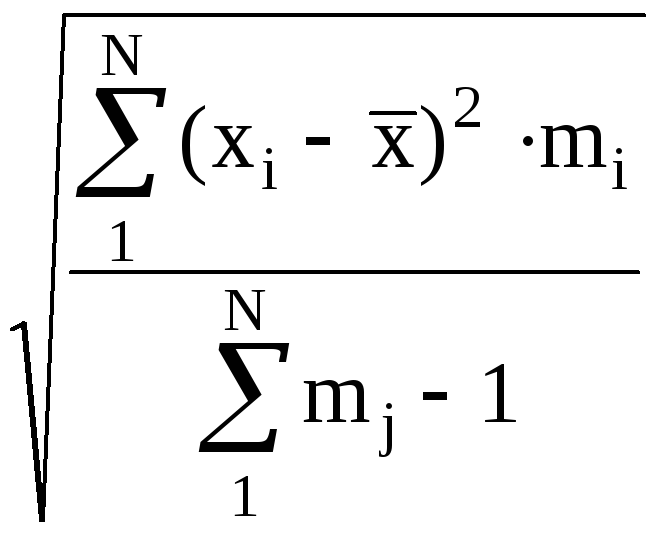 (2.11)
(2.11)
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«Юго-Западный государственный университет»
Кафедра финансов и кредита
Лабораторная работа №1
Методы группировки статистических данных
студент 1 курса
группы ЭБ-21 Гревцева Наталья
к.э.н., ст. преподаватель Обухова Анна Сергеевна
Курск 2013
Выборочный метод.
Статистическое распределение выборки
При изучении величины, принимающей случайные значения (результатов физических измерений в серии экспериментов, экономических показателей, параметров технологических процессов и т.п.), мы имеем дело с выборками. Выборочное наблюдение – это способ наблюдения, при котором обследуется не вся совокупность значений изучаемой величины, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью или выборкой, а всю совокупность единиц, из которых производится отбор, — генеральной совокупностью.
Существуют различные способы формирования выборки (случайный, механический, типический, серийный (гнездовой)), но в математической статистике изучается собственно-случайная выборка с повторным отбором или бесповторным отбором.
Собственно-случайная выборка формируется с помощью жеребьевки либо по таблице случайных чисел. Всем элементам генеральной совокупности присваиваются порядковые номера, затем производится выбор случайных номеров с помощью датчиков случайных чисел или из специальных таблиц, которые образуют порядковые номера для отбора.
При повторном отборе единица наблюдения после извлечения из генеральной совокупности регистрируется и вновь возвращается в генеральную совокупность, откуда опять может быть извлечена случайным образом.
При бесповоротном отборе элемент в выборку не возвращается.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности n.
Если объем генеральной совокупности велик, то разница между повторной или бесповторной выборками незначительна.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Сущность выборочного метода заключается в том, что выводы, сделанные на основе изучения части совокупности (случайной выборки), распространяются на всю генеральную совокупность. Математическая статистика занимается обоснованием такого приема, применяя теорию вероятностей.
Вариационный ряд
Элементами выборки < 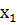 ,
, 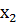 …,
…, 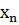 > являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (a,b). Другими словами, выборка может быть частью генеральной совокупности, которая соответствует дискретной или непрерывной случайной величине.
> являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (a,b). Другими словами, выборка может быть частью генеральной совокупности, которая соответствует дискретной или непрерывной случайной величине.
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если выборка соответствует дискретной случайной величине, то вариационный ряд представляет собой таблицу, которая ставит в соответствие каждому значению 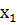 его частоту
его частоту 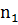 . Такой ряд носит название дискретный вариационный ряд.
. Такой ряд носит название дискретный вариационный ряд.
Например, на основе наблюдения за ростом растения получены n=50 значений числа почек на единицу длины ветки (пример 3.1, табл.3.2). Понятно, что здесь мы имеем пример дискретной случайной величины, так как число почек может быть только целым.
Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала (a,b), то строим интервальный вариационный ряд с помощью группировки вариант.
Существуют различные способы группировки вариант, среди которых является метод равных интервалов.
Рассмотрим алгоритм группировки методом равных интервалов.
1. Сначала определяют число интервалов m. Для этого обычно применяют формулу Стреджесса:
m = 1 + 3,22 × lg n. (3.1)
Число m округляют до целого значения.
Приведем еще несколько формул расчета числа интервалов:
m = 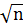 — 0,013n , (3.1a)
— 0,013n , (3.1a)
m = 1,72 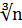 (3.1b)
(3.1b)
m = 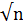 + 1. (3.1c)
+ 1. (3.1c)
В программе Excel есть процедура «Гистограмма», которая умеет строить вариационный ряд и вычисляет число интервалов по формуле (3.1с). Пример применения процедуры «Гистограмма» приведен ниже.
В табл. 3.1 вычислены рекомендуемые формулами (3.1), (3.1а), (3.1b) и (3.1с) числа интервалов. Значения приведены с округлением до целого.
Таблица 3.1
| Объем выборки n | Рекомендуемое число интервалов | ||
| формула 3.1 | формула 3.1а | формула 3.1b | формула 3.1 с |
| 3,723 | 2,555 | 3,29 | 3,646 |
| 4,965 | 3,902 | 4,423 | 5,123 |
| 5,612 | 4,845152 | 5,16 | 6,196 |
| 6,053 | 5,602 | 5,731 | 7,083 |
| 6,388 | 6,245 | 6,207 | 7,856 |
| 6,658 | 6,809 | 6,619 | 8,55 |
| 6,884 | 7,314 | 6,986 | 9,185 |
2. Далее вычисляют границы интервалов.
Приведём два способа определения границ.
В первом способе длину интервала вычисляют по формуле.
h= 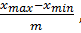
xmin=min i>, xmax=i>, (3.2a) и определяют границы интервалов по формулам:
При таком выборе хmin попадает в середину первого интервала, а xmax – в середину последнего, и число интервалов m.
Во втором способе длина интервала и границы вычисляются по формулам:
h= 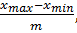 (3.2б)
(3.2б)
При этом хmin относится к первому, а xmax – к последнему интервалам.
h= 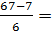 10
10
3. После определения границ интервалов вычисляют для каждого j-того интервала
Xср.j 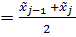 (3.4)
(3.4)
и частоту nj т.е. число таких элементов xi выборки, которые удовлетворяют условиям
 j-1 накопл =
j-1 накопл = 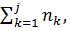 wj накопл =
wj накопл = 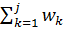 =
= 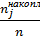 , j= 1,…,m. (3.7)
, j= 1,…,m. (3.7)
Вариационный ряд записывают в виде таблицы (табл.3.2)
Приведем два способа определения границ.
В первом способе длину интервала определяют по формуле.
h= 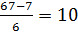 , xmin= mini>, xmaxi>, (3.2a)
, xmin= mini>, xmaxi>, (3.2a)
определяют границы интервалов по формулам:
При таком выборе xmin попадет в середину первого интервала, а xmax — в середину последнего, и число интервалов равно m.
Во втором способе длина интервала и границы вычисляются по формулам:
h= 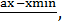 (3.3а)
(3.3а)
При этом хmin относят к первому, а хmax — к последнему интервалам
Таблица 3.2
| Номер интервала j | Интервал ( 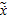 j-1, j-1, 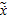 j] j] |
Середина интервала Xср.j | Частота nj | Накопленная частота nj накопл | Частость wk | Накопленная частость wj накопл |
| (2,12] | 0,14 | 0,14 | ||||
| (12,22] | 0,24 | 0,38 | ||||
| (22,32] | 0,33 | 0,71 | ||||
| (32,42] | 0,43 | 1,14 | ||||
| (42,52] | 0,53 | 1,67 | ||||
| (52,62] | 0,63 | 2,3 |
Замечание. Вариационный ряд можно задать двумя столбцами: интервалами (или их серединами) и частотами. Остальные столбцы легко вычисляются.
При повторном отборе единица наблюде6ния после извлечения из генеральной совокупности регистрируется и вновь возвращается генеральная совокупность, откуда опять может быть извлечена случайным образом.
При бесповторном отборе элемент в выборку не возвращается.
Число единиц (Элементов) статистической совокупности называется ее объемом. Объем генеральн6ой совокупности обозначается N, а объем выборочной совокупности n.
Если объем генеральной совокупности велик, то разница между повторным или бесповторными выборками незначительна.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Сущность выборочного метода заключается в том, что выводы, сделанные на основе изучения части совокупности (случайной выборки), распространяется на всю генеральную совокупность. Математическая статистика занимается обоснованием такого приема, применяя теорию вероятности.
Гистограмма, полигон, кумулята и огива
Для графического изображения вариационного ряда используются гистограмма, полигонов, кумулята и огива.
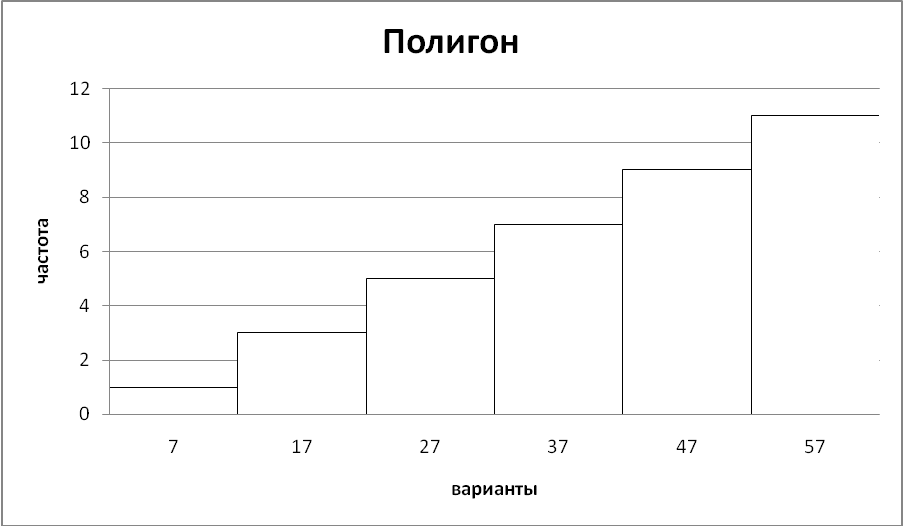
Для дискретного вариационного ряда полигон частот представляет собой многоугольник (рис. 3.1), ограниченный осью ОХ и ломанной, соединяющей точки ( 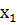 ,0), (
,0), ( 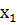 ,
, 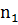 ), (
), ( 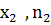 ),…,(
),…,( 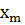 ,
, 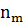 ), (
), ( 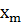 ,0)
,0)
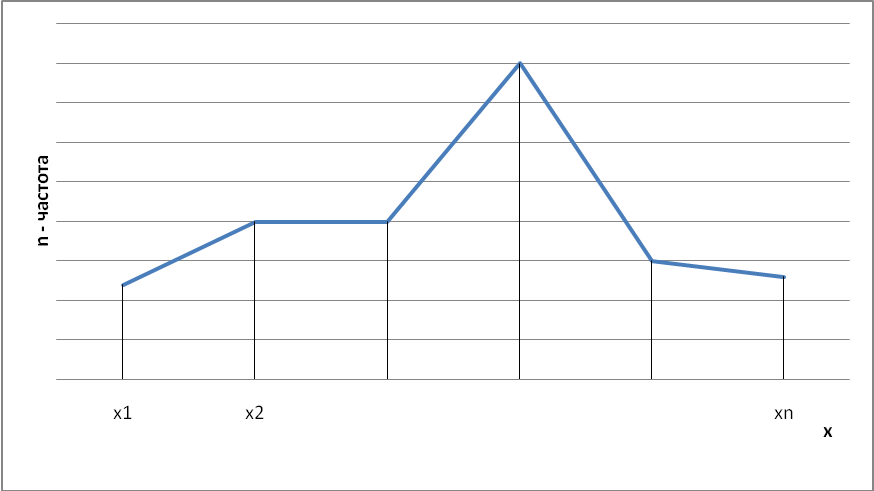
Для интервального вариационного ряда с равными интервалами гистограмма частот состоит из прямоугольников, ширина которых равна длине интервала, а высота пропорциональна частоте (рис. 3.2). Для интервального ряда с неравными интервалами ширина прямоугольника равна длине соответствующего интервала, а высота пропорциональна плотности частоты, равной отношению частоты к длине интервала.
В общем случае гистограмма состоит из прямоугольников, ширина каждого из которых равна длине соответствующего интервала, а площадь прямоугольников пропорциональна частоте или относительной частоте. При этом сумма площадей всех прямоугольников равна сумме частот или единице.
Обычно гистограмму состоят по относительным частотам, так чтобы сумма площадей прямоугольников была равна единице. Тогда ломаная, соединяющая середины верхних сторон прямоугольников (полигон), является аналогом графика плотности вероятностей распределения.
При больших объемах выборки полигон относительных частот приближенно отображает график функции плотности вероятностей генерального распределения.
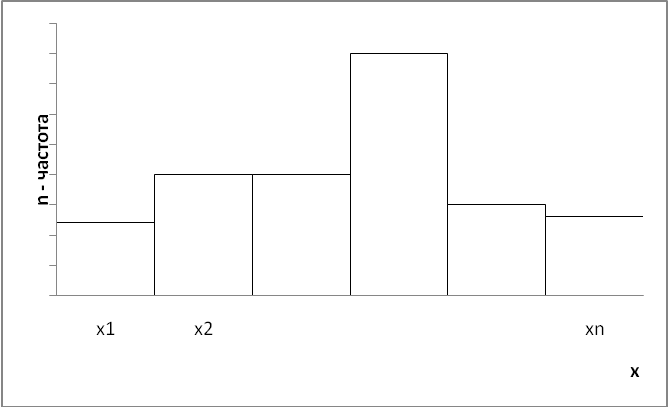
Полигон накопленных частот строится так же, как и полигон частот, при этом вместо частот используются накопленные частоты.
Для непрерывного признака на оси абсцисс откладываются значения середин интервалов, а на оси ординат – накопленные частоты или накопленные частости. Полученные точки соединяют гладкой кривой, которая называется кумулятивной кривой (или кумулятой). Кумулята, построенная по накопленным частотам, при больших объемах выборки является приближением к графику функции распределения вероятностей генеральной совокупности.
Огива в англоязычной литературе определяется как сглаженный график накопленных частот, т.е. это кумулята.
В российских учебниках по статистике огива определяется по-разному.
В одном случае огива — это ломаная, соединяющая точки, полученные при откладывании значений вариант на оси ординат, а накопленные частот — на оси абсцисс (Шмойлова Р. А., Минашкин В. Г., Садовникова Н. А., Шувалова Е. Б. Теория статистики: учебник,М.: Финансы и статистика, 2006).
В другом случае огива строится так же, как и кумулята, только вместо накопленных частот используются частоты, подсчитанные с условием «больше чем» (Теория статистики: учебник / под ред.: «проф. Г. Л. Громыко. — М.: ИНФРА-М, 2000).
Таблица 3.2
| Номер интервала j | Интервал (хо-1,хj] | Середина интервала | Частота n | Накопленная частота Nj накопл. |
| (2,12] | ||||
| (12,22] | ||||
| (22,32] | ||||
| (32,42] | ||||
| (42,52] | ||||
| (52,62] |
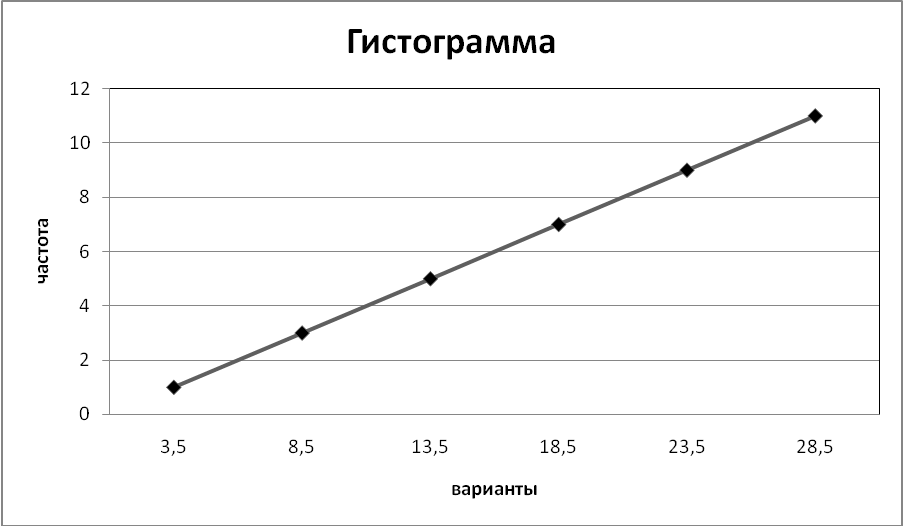
Введем в программе Excel исходные данные из таблицы 3.2 и построим полигон (рис.3.3) и гистограмму (рис. 3.4).
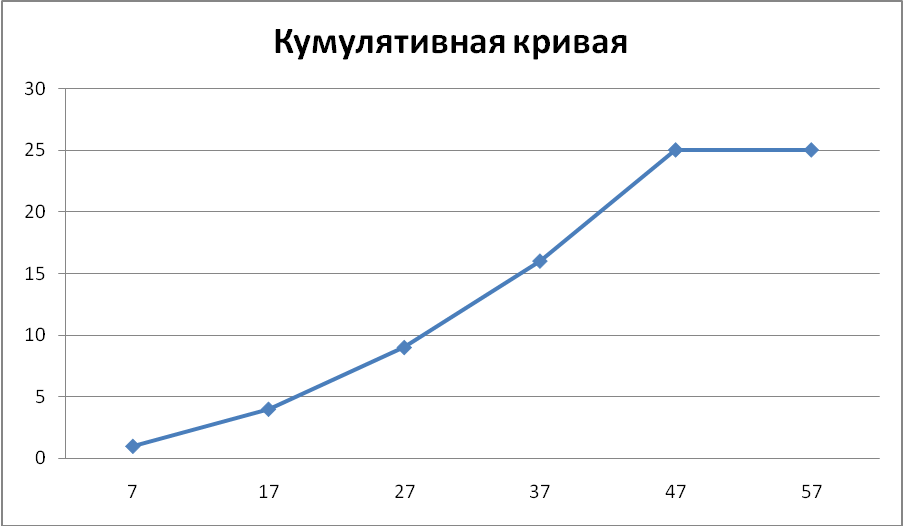
Построим кумулятивную кривую. Введем варианты и накопленные частоты в Exel, выделим диапАзон A1:B2, выберем тип диаграммы «Точечная диаграмма со значениями, соединенными сглаживающими линиями». После преобразований получим диаграмму, изображенную на рис. 3.5.
Если мы просто поменяем местами столбцы A1 :A6 и B1: B6, то диаграмма преобразуется в огиву. После замены заголовка и форматирования осей получим диаграмму на рис. 3.6. Эта кривая соответствует определению огивы из первого из указанных выше учебников.
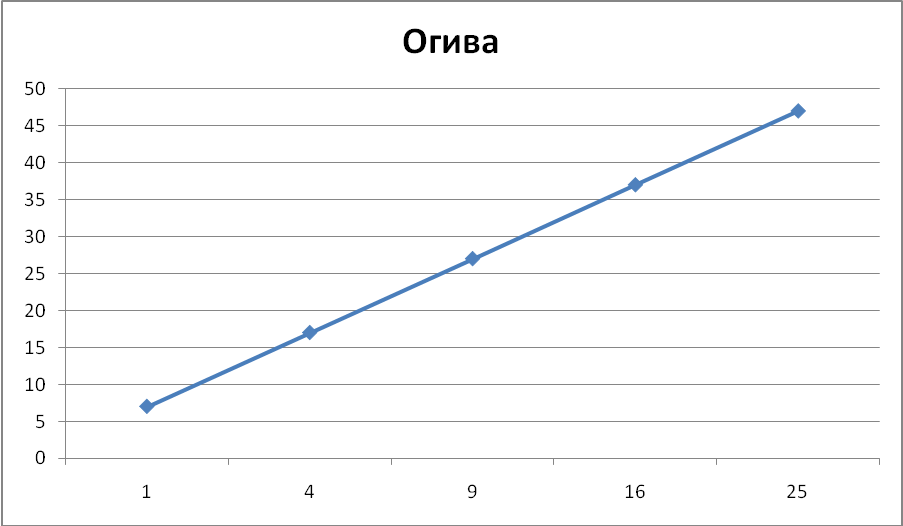
В одном случае огива – это ломаная, соединяющая точки, полученные при откладывании значений вариант на оси ординат, а накопленных частот – на оси абсцисс (Шмойлова Р.А., Минашкин В.Г., Садовникова Н.А., Шувалова Е.Б. Теория статистики: учебник. – М.: Финансы и статистика, 2006).
В другом случае огива строится так же, как и кумулята, только вместо накопленных частот используются частоты, подсчитанные с условием «больше чем» (Теория статистики: учебник / под ред. проф. Г.Л. Громыко. – М.: ИНФРА-М,2000).
Значения каждого из трех признаков должны быть упорядочены, что реализуется с помощью сортировки (отдельно каждого из признаков): выбираем вкладку ДАННЫЕ – СОРТИРОВКА (традиционно по возрастанию).
Для выполнения структурной равноинтервальной группировки сначала определяем величину интервала по формуле:

где R – размах вариации, 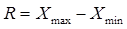 ;
;
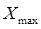 — максимальное значение группировочного признака;
— максимальное значение группировочного признака;
 — минимальное значение группировочного признака;
— минимальное значение группировочного признака;
Число групп определяется следующими факторами: задачами исследования, основанием группировки, численностью совокупности, степенью вариации (изменчивости) признака.
Как ориентир для определения количества групп может быть использована формула Стерджесса:

где N – число единиц совокупности.
Если признак варьирует незначительно, может быть взято и меньшее число групп. И наоборот, если вариация велика, для более подробного ее описания лучше выбрать большее число групп.
Далее определяются границы каждого интервала по следующей схеме:
| № интервала | Границы интервала | |
| нижняя | верхняя | |
 |
 |
|
 |
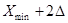 |
|
| … | ||
| k |  |
 |
Например, пусть статистическая совокупность состоит из 40 туристических компаний, показатели выручки которых варьируют от 50 млн. у.е./год до 650 млн. у.е./год, что является, соответственно, минимальным и максимальным значениями признака. Тогда по формуле Стерджесса получаем:  . Величина интервала для построения равноинтервальной группировки определяется следующим образом:
. Величина интервала для построения равноинтервальной группировки определяется следующим образом:  (млн.у.е.). Таким образом, совокупность компаний будет разделена по показателю выручки на шесть равных групп: [50-150], [150-250], [250-350], [350-450], [450-550], [550-650] (млн. у.е./год).
(млн.у.е.). Таким образом, совокупность компаний будет разделена по показателю выручки на шесть равных групп: [50-150], [150-250], [250-350], [350-450], [450-550], [550-650] (млн. у.е./год).
После определения границ интервалов рассчитываются частоты, для чего используется функция ЧАСТОТА(вводится как формула массива, т.е. комбинацией клавиш CTRL + SHIFT + ВВОД). Выделяем столбец, в который должны поместиться частоты, соответствующие каждому интервалу. Вызываем функцию (из категории «Статистические») :
= ЧАСТОТА(массив_данных;массив_интервалов)
где массив_данных – это столбец исходных значений признака, для которых вычисляются частоты;
массив_интервалов – это столбец верхних границ интервалов с 1-го по k-1 –й (т.е. без последнего). Функция ЧАСТОТА предполагает формирование верхних границ по принципу «включительно», а нижних – «исключительно».
Сумма частот должна быть равна объему совокупности:

где  — число наблюдений (частота) в i – ой группе.
— число наблюдений (частота) в i – ой группе.
Далее оценивается относительная структура совокупности через расчет частостей:


где  — частость в i – ой группе, выраженная в долях единицы или в процентах к итогу.
— частость в i – ой группе, выраженная в долях единицы или в процентах к итогу.
В результате получаем структурную равноинтервальную группировку.
Группировки с равными интервалами предпочтительнее, но характер изменения большинства социально-экономических явлений не отвечает требованиям, предъявляемым к равноинтервальной группировке.
Если в результате построения равноинтервальной группировки большая часть совокупности попала в один-два смежных интервала, а остальные содержат незначительное число наблюдений, это свидетельствует о том, что исследуемый признак варьирует неравномерно. В данном случае может быть использован «прогрессивный» подход к определению границ интервалов.
В этом случае величина интервалов определяется формулами:


где  — величина i+1 – го интервала;
— величина i+1 – го интервала;
 – константа арифметической прогрессии, для возрастающих интервалов
– константа арифметической прогрессии, для возрастающих интервалов  , для убывающих интервалов
, для убывающих интервалов  ;
;
q – константа геометрической прогрессии, для возрастающих интервалов  , для убывающих интервалов
, для убывающих интервалов 
Описанные выше технические способы определения величины интервалов не гарантируют, что не появятся группы малочисленные или вообще «пустые», в которые не попало ни одно наблюдение. Если это произошло, необходимо изменить число групп и/или величины интервалов, так как подобная группировка является некорректной.
Для обеспечения статистической устойчивости показателей, исчисляемых для отдельных групп, может использоваться равнонаполненная группировка, в которой число наблюдений в каждой группе примерно одинаковое и определяется по формуле:
 .
.
Если полученное n не целое и/или в совокупности есть повторяющиеся значения признака, то число наблюдений в каждой группе может различаться. При этом надо стремиться к тому, чтобы эти различия были незначительны.
Если для реализации задач исследования необходимо устанавливать границы групп там, где количество переходит в новое качество, пользуются специализированными интервалами.
Границы групп могут определяться и произвольно, когда ни один из вышеописанных методов не дал хороших результатов.
В результате на основе итоговой группировки формируется вариационный ряд распределения (см. табл. 1).
Таблица 1. Ряд распределения выручки туристических компаний, млн. у.е./год
| Границы интервала | Частота | Частость | Плотность абсол. | Плотность отснос. |
| нижняя | верхняя | |||
| 0,300 | 0,12 | 0,00300 | ||
| 0,250 | 0,10 | 0,00250 | ||
| 0,200 | 0,08 | 0,00200 | ||
| 0,125 | 0,05 | 0,00125 | ||
| 0,100 | 0,04 | 0,00100 | ||
| 0,025 | 0,01 | 0,00025 | ||
| Итого | — | — |
Для неравноинтервального вариационного ряда распределения сравнение частот по группам неправомерно. В данном случае необходимо избавиться от влияния величины интервала путем перехода от частот/частостей к абсолютной/относительной плотности распределения:


где  — абсолютная плотность распределения в i – ой группе;
— абсолютная плотность распределения в i – ой группе;
 — относительная плотность распределения в i – ой группе;
— относительная плотность распределения в i – ой группе;
 — величина i – го интервала.
— величина i – го интервала.
Далее строится кумулятивный ряд распределения, для чего рассчитываются накопленные частоты/частости к концу каждого интервала:


где  /
/  — накопленная частота/частость к концу i – ой группы.
— накопленная частота/частость к концу i – ой группы.
Построение гистограммы и кумуляты выполняется с указанием названия графика и каждой оси. Для кумуляты в таблице рассчитываем накопленные частоты/частости (см. табл.2):


где  /
/  — накопленная частота/частость к концу i – ой группы.
— накопленная частота/частость к концу i – ой группы.
Таблица 2. Кумулятивный ряд распределения выручки туристических компаний, млн. у.е./год
| Границы интервала | Частота | Частость | Накопленная частота | Накопленная частость |
| нижняя | верхняя | |||
| 0,30 | 0,300 | |||
| 0,25 | 0,550 | |||
| 0,20 | 0,750 | |||
| 0,13 | 0,875 | |||
| 0,10 | 0,975 | |||
| 0,03 | ||||
| Итого | — | — |
Гистограмма– графическое изображение интервального вариационного ряда распределения, дающее представление о характере изменения его частот (рис. 1).
Для построения гистограммы выбираем вкладку ВСТАВКА и из разновидностей диаграмм MS Excel — ГИСТОГРАММА. На оси абсцисс откладываются величины интервалов значений признака, на оси ординат – частоты, частости или плотности распределения. Для равноинтервальных рядов могут быть использованы и частоты/частости, и плотности, для неравноинтервальных – только плотности.

Рис. 1. Гистограмма распределения выручки туристических компаний

Рис. 2. Кумулята распределения выручки туристических компаний
Кумулята – графическое изображение кумулятивной кривой, дающее представление о характере изменения накопленных частот/частостей (рис. 2).
Для построения кумуляты выбираем ВСТАВКА и из разновидностей диаграмм MS Excel – ТОЧЕЧНАЯ(с прямыми отрезками). На оси абсцисс откладываются величины интервалов значений признака, на оси ординат — накопленные частоты или частости. Равенство или неравенство интервалов для графика кумуляты значения не имеет.
Выводы должны давать общую картину распределения: однородность совокупности («похожесть» единиц совокупности друг на друга), концентрация значений вокруг средней величины, «типичное» значение, симметричность распределения (преобладание больших или малых значений).

